将光线从相机投射到图像平面上
在现实世界中,光线来自光源,与物体碰撞,导致反射光线向多个方向散射。一些反射光线进入我们的眼睛——照相机——这就是我们看到的光线。如果我们要忠实地模拟这一点,我们将模拟许多我们从未见过的光线,这是对计算能力的浪费。相反,在光线追踪中,我们往回走:将光线从相机投射到外面的世界,看看它们是如何到达光源的。
在前向追踪中,大多数光线不会到达相机。在反向追踪中,我们只考虑从相机开始到相机结束的光线
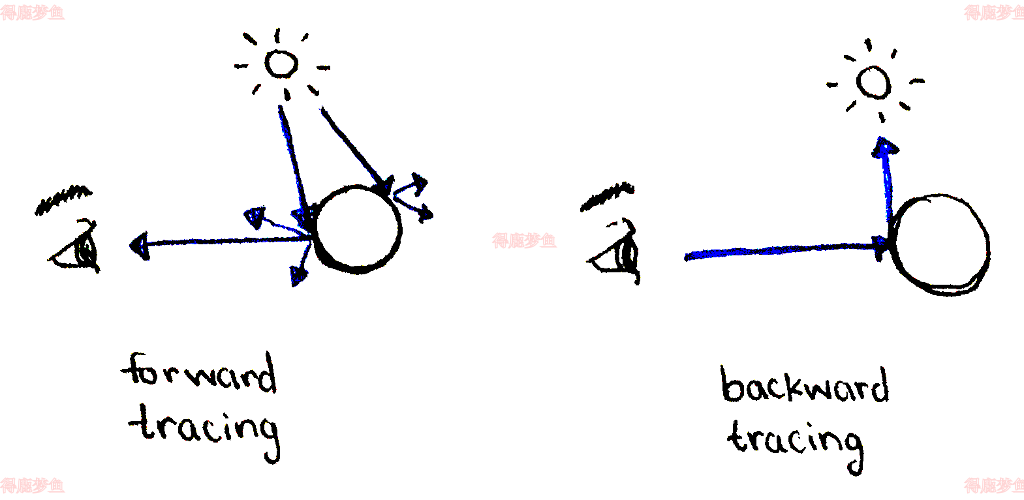
即使用回溯的方法,我们投射了多少光线,哪些光线?为了回答这个问题,我们将图像平面划分为小区域,一个对应于输出图像中的每个像素。然后,我们构造一条从摄像机出发并穿过每个区域中心的射线
这样就构造了一条射线,它从相机出发,经过成像平面上的一点, 如下图所示
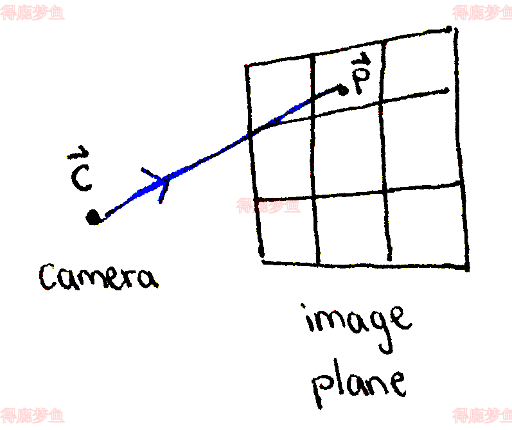
摄像机的位置是恒定的;我们称之为c, 图像平面由四个角的位置表示,称之为四个角x0,x1,x2,x3, 假设我们有一个点p在成像平面上。这个点是某个百分比α∈[0,1]
双线性插值
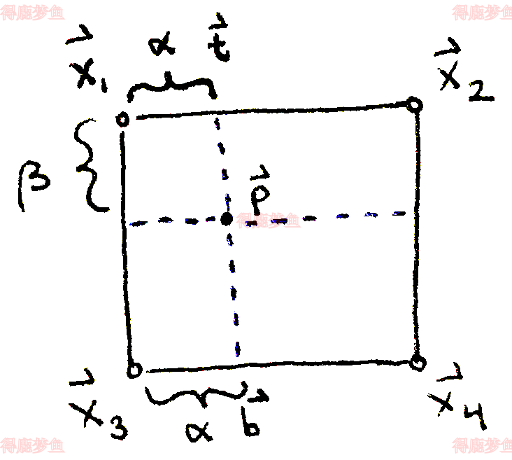
⎩⎨⎧t=αx2+1−αx1b=αx4+1−αx3p=βb+1−βt双线性插值
对矢量的快速复习
三维空间中的一个点可以表示为沿三个轴的距离。这些距离被称为坐标。坐标轴,标记为x,y和z,按照惯例,排列在右手坐标系中。
为了区分矢量和标量(非矢量的数值),我们将用粗体写出矢量的名称,并在顶部加一个箭头。一个向量也可以写成尖括号内的三个分量。
V=x,y,z或者V=⟨x,y,z⟩
两个向量的和是由两个向量从坐标系的原点依次跟随得到的向量。这两个矢量的差是由从第二个矢量的尖端开始并移动到第一个矢量的尖端得到的矢量,也就是平行四边形法则或者三角形法则
向量可以通过标量缩放,拉伸或压缩向量。该操作通过将向量的每个坐标按标量缩放来执行(向量的数乘)
实现
构建基本的基础结构
构建渲染平面
用四个向量表示场景中的图像平面:x1, x2, x3, x4
一个好的位置是:
x1=⟨1,1,0⟩x1=⟨−1,1,0⟩x1=⟨1,1,0⟩x1=⟨−1,−1,0⟩
确定将光线投射到哪里
计算公式参考双线性插值公式
