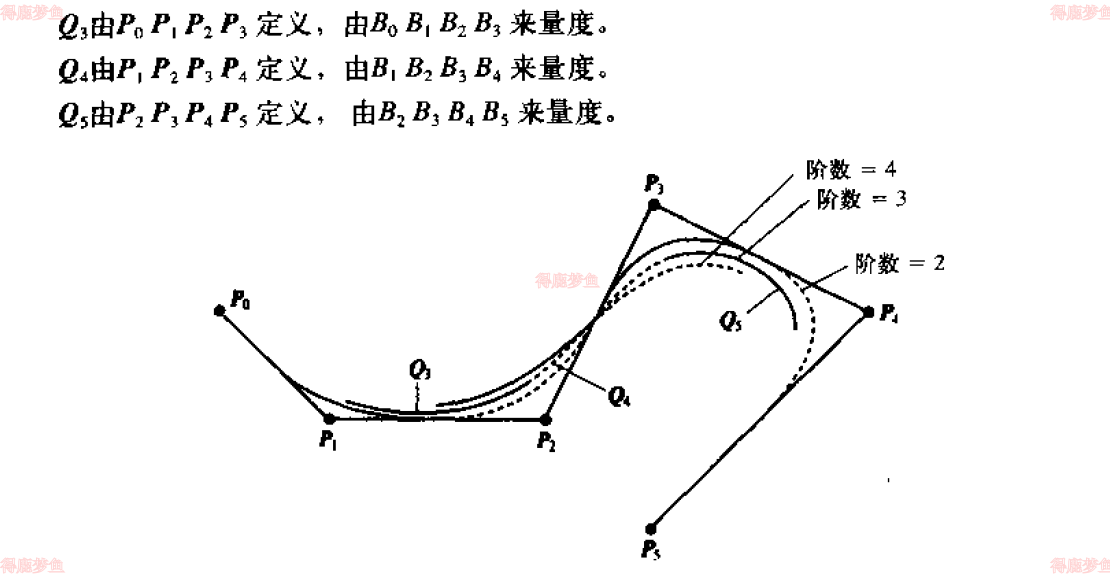
bezier曲线

bezier曲线的开发工作是20世纪60年代在雷诺汽车公司进行的

bezier曲线是一个多项式，多项式的阶数总是比控制点的个数少一，在计算机图形学中，我们一般采用三阶。四阶曲线的灵活性不足，而且超过三阶时，复杂性增加，所以选择三阶对于大多数的计算图形学应用是最好的折中方案

曲线遵循控制点多边形的形状。并且被限制在控制点形成都凸包内

控制点并不对局部进行控制，移动任何控制点都会影响曲线上的所有点，只是影响作用或大或小。

第一个和最后一个控制是曲线段的端点

在端点出曲线的切向量与控制点多边形的第一条和最后一条边相重合

移动控制点会改变切向量的大小和方向，这是bezier曲线接口的直观感觉的基础

曲线关于任意直线的震荡并不会比关于控制点多边的震荡多，这种性质被称为变异消失性，这个性质具有可以表示的表面本性的含义

通过对其控制点表示应用任意的仿射变换。可以变换曲线。在这样的变换下，曲线是不变的（不改变形状）

B样条线

两个bezier曲线所具有但被B样条曲线克服的缺陷是其非局限性以及曲率和控制点数据之间的关系。第一个性质（非限制性）是指，尽管控制点对最靠近它的那一部分曲线有非常大的影响，但它也会对整条曲线有影响，第二缺点是在不采用多个曲线段（或者通过增加曲线的曲率）的情况下，我们就不能用一个bezier三次曲线来近似或表示n个点
与bezier曲线一样，B样条曲线不通过其控制点，B样条曲线是由任意数量的曲线段组成的弯曲的分段三次多项式（为了表示上的方便，我们只讨论三次B样条，但是B样条可以有任意阶的）公式如下：
$Q_iu=UB_sP = [u^3u^2u]\frac{1}{6}\left [\begin{matrix}-1 & 3 & -3 & 1 \\3 & -6 & 3 & 0 \\-3 & 0 & 3 & 0 \\-1 & 4 & 1 & 0 \end{matrix}\right]\left [\begin{matrix}P_{i-3} \\P_{i-2} \\P_{i-1} \\P_{i} \end{matrix}\right]$
其中 $Q_i$ 是第i个B样条曲线，P是按照控制点顺序排列的一个四个点的集合，
对于B样条曲线，每一个曲线段都是由4个控制点来定义的，而且每一个控制点会影响4个并且只4个曲线段这就是B样条曲线的局部特性。同时也是主要优点

需要注意：将bezier曲线和B样条曲线进行比较可能会引起误解，因为这种比较不是在相同性质的进行的，而是将一个bezier曲线的片段与以整段B样条器宇轩曲线或者一个合成的B样条曲线进行比较。一个bezier曲线是受全局控制的，因为移动一个控制点会影响整条曲线，而在一条合成的B样条曲线上，移动一个控制点只影响该曲线中的几个片段。
B样条曲线表现出位置连续性，一阶导数连续性和二阶导数连续性，能够获得这种性质是因为基函数本事二阶可导的多项分布式，

均匀B样条曲线

$Q_iu=\sum^3_{k=0}p_{i-3+k}B_{i-3+k}u$
i为片段数，k为局部控制点的下表，也就是片段i的下标,在一个曲线段上的u值是0到1之间的闭区间。

B样条曲线中的每一个片段都有4个基函数和4个控制顶点来定义。因此，就有比曲线段多出来的三个基函数和三个控制点，在片段之间u值上的连续点被称为结点值。均匀B样条是这结点值对于参数u是等间距的。

由6个控制点定义的3段B样条三次曲线

非均匀样条曲线

非均匀B样条是一种连续结点值之间不一定相等的曲线，这就是弯曲函数不载是可以互相平移的。而是区间和区间可能不相等。非均匀B样条的最常见形式是通过插入多个结点使得连续的结点值区间中的某些区间减少到零。

性质

曲线遵循控制点多边形的形状，并且被限定在由有控制点组成的凸包中
曲线显示了变异消失性
通过对其控制点表示应用任意仿射变换可以变换曲线
B样条曲线表现出局部控制性--一个控制点与4个片段相连在三阶而移动一个控制点可以只影响其中的几个片段

有理曲线

有理曲线是在四维空间定义的曲线，该空间称为投影空间。接着在将其投影到三维空间中。

有理Bezier曲线

将一条三维的Bezier曲线投影到二维空间。特别是投影到z=1的平面。曲线公式为
$Ru=\{\frac{xu}{zu}, \frac{yu}{zu}\}$
在三维投影空间定义的曲线
$QU=\sum^3_{i=0}P_iB_iu \\P_i=x_i, y_i, z_i$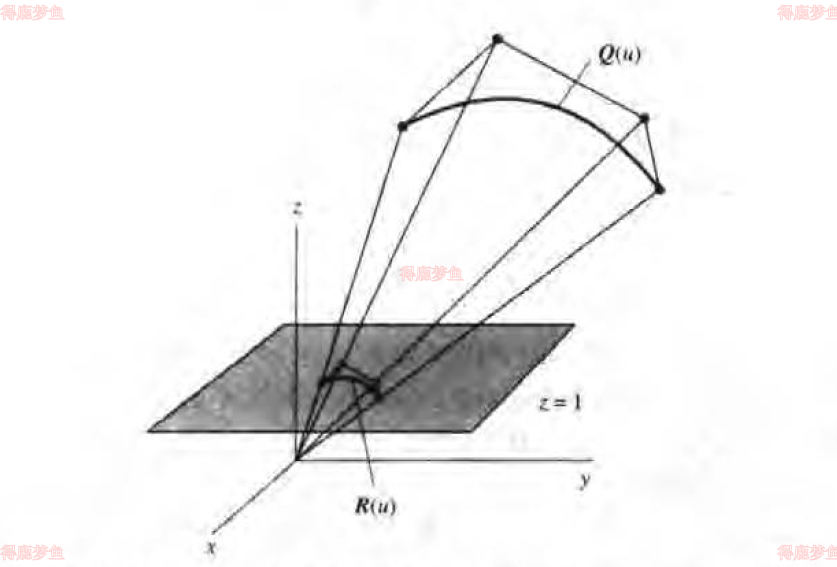
三维bezier曲线投影到到z=1的平面

使用一种特殊的表示方法来描述二维空间中一条有理曲线的三维控制点
$P_i=w_ix_i, w_iy_i,w_i$

三维曲线可表示为
$Qu=\sum^3_{i=0}\left[\begin{matrix}w_ix_i \\w_iy_i \\ w_i\end{matrix}\right]B_iu$
投影二维平面后为
$Ru=\{\frac{\sum w_ix_iB_iu}{\sum w_iB_iu} ,\frac{yu}{\sum w_iB_iu}\} \\P_i=w_ix_i, w_iy_i,w_iz_i,w_i$

NURBS

NUBRS表示非均匀有理B样条Non-Uniform Rational B-Spline；这种表示在CAD中最通用。在设计应用程序中，可以有一下的可能性

控制点的交互式放置和移动
结点的交互式放置和移动
控制点权重的交互式控制

把有理曲线的有点和非均匀B样条的性质相结合，可以吧NUMBRS曲线定义为内部结点间跨度不均匀的结点向量上的非均匀的结点向量上的非均匀B样条曲线。

控制点的集合定义 $P^w_i=w_ix_i,w_iy_i,w_iz_i,w_i$

从曲线到表面

三次Bezier曲线片定义为 $Qu,v=\sum^3_{i=0} \sum^3_{j=0} P_{ij}B_iuB_jv$

从数学上讲，三维表面被认为是由2条曲线的笛卡尔积而产生的。

多面体

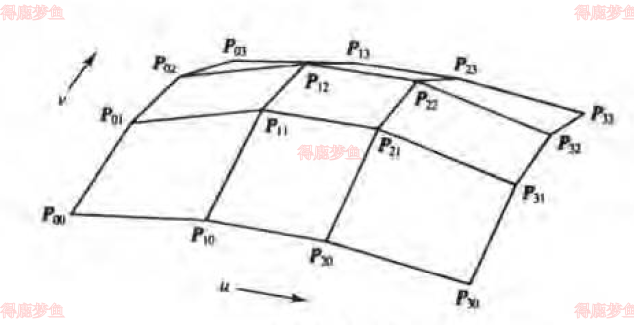
与bezier曲线中的控制点类似，曲面片有4个端点，8个切向量以及4个扭向量来定义