数字图像处理基础知识

图像的概念

图像是与之对应的景物的一个表示，一幅三维空间、动态的图像可以表示为$I=fx,y,z,t$,I是物体辐射能量，$x,y,z$是空间变量，$t$是时间变量。在实际应用中，图像可以借助不同的方式获得，得。目前普遍采用的一种方式是利用一定波谱段内的电磁能量来成像，可从可见光扩展到其他频段。在低频端，有红外线、微波等；在高频端，有紫外线、Ｘ射线、$\gamma$射线、宇宙射线。
考虑到某一波谱段内的电磁能量成像，图像可以表示为$I=fx,y,z,\lambda,t$

一幅图像记录的是物体辐射能量的空间分布，一般表示成灰度图，这时$f$为辐射度对应的灰度值。当对可见光成像时，灰度值对应客观景物被观察到

一般情况下只考虑平面、单色、静止图像，此时图像可表示为一个二维函数
$I=fx,y$

数字图像表示

传统意义上的图像是连续的，即上式中的$x,y,f$是连续的，$x,y$连续表示的是空间中点的连续，$f$连续表示的是物体辐射能量在空间中的分布连续，连续图像也称为模拟图像

为了便于利用计算机对图像进行进一步的加工和处理，需要把模拟图像在空间上、幅值上进行离散化，将其转换为对应的数字形式。离散化的图像称为数字图像。图像的离散化过程包括两种处理：取样和量化。一幅模拟图像的坐标及幅度都是连续的，为了把它转换为数字形式，必须对坐标和幅度都做离散化操作。数字化坐标值称为取样，它确定了图像的空间分辨率；数字化幅度值称为量化，它确定了图像的幅度分辨

坐标约定

取样和量化的结果是一个实数矩阵，我们主要使用两种方法来表示数字图像，假设一幅图像$fx,y$取样后，得到了一幅M行N列的图像，我们称这幅图像的大小为$M \times N$。坐标$x,y$的值是离散量

以均匀取样为例，模拟图像的取样过程如下图,假设沿空间$x$轴方向的取样间隔为等间距$\Delta x$，沿$y$轴方向的取样间隔为等间距$\Delta y$，则均匀取样过程可看作将图像平面划分为规则、均匀的网格，每个网格的位置由$x,y$表示，ｘ的取值范围为［0, M-1］,Ｍ为沿$x$方向的取样点数；$y$的取值范围为［0，N-1］,Ｎ为沿$y$方向的取样点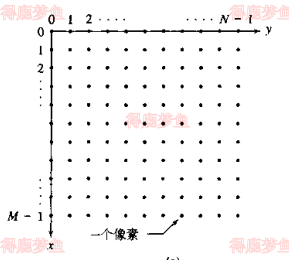

对于一维信号的取样过程来说，为了准确恢复出实际信号，必须满足香农取样定理。同样地，从取样图像中恢复原来的图像也需要满足二维取样定理

$$\begin {cases}\Delta x \leq \frac{1}{2\omega_u} \\\Delta y \leq \frac{1}{2\omega_v}\end {cases}$$

$\omega_u, \omega_v$分别为$x,y$方向上的最高空间

对于灰度图像，量化是对取样所得的离散样本点的灰度值进行离散化，将原图像的连续灰度用$L=2^k$（ｋ为整数）个等间距的灰度级进行表示。连续图像被取样与量化后可以用一个Ｍ×Ｎ矩阵来表示，即

$$fx,y = \begin{bmatrix}f0,0 & f0,1 & \cdots & f0, N-1 \\f1,0 & f1,1 & \cdots & f1, N-1 \\\vdots & \vdots & \ddots & \vdots\\fM-1,0 & fM-1,1 & \cdots & fM-1, N-1 \\\end{bmatrix}$$

此时，等式左边的$fx,y$被称为数字图像，矩阵中的每一个元素的坐标点代表图像的一个像素pixel

对于一幅数字图像，存储图像需要的比特 $b=M*N*k$

根据颜色的不同，可以将图像分为以下

图像类型

灰度图像

当一幅图像有$2^k$个灰度级时，通常称该图像是ｋ比特图像。例如，一幅图像有256个可能的灰度级，则称其为8比特图像。灰度图像中矩阵元素的取值范围通常为［0，255］，因此其数据类型一般为8位无符号整数，这就是人们经常提到的256级灰度图像。0表示纯黑色，255表示纯白色，中间的数字从小到大表示由黑色到白色的过渡

二值图像

二值图像的灰度值只由0、1两个值构成，0代表黑色，1代表白色。由于每一个像素的取值仅有0、1两种可能，所以计算机中二值图像的数据类型通常为一个二进制位。二值图像通常用于文字、线条图的扫描识别（OCR）和掩模图像的存储。二值图像可以看作灰度图像的一个特例

彩色图像

RGB图像可以用来表示彩色图像。它分别用红色（R）、绿色（G）、蓝色（B）三基色的组合来表示每个像素的颜色，图像中每一个像素的颜色值（由RGB三基色表示）直接存放在图像矩阵中。由于每一个像素的颜色需要由R、G、B三个分量来表示，因此RGB像的图像矩阵与其他类型的图像矩阵不同，是一个三维矩阵。可用$M\times N \times 3$，Ｍ、Ｎ分别表示图像的行、列数，3个$M\times N$的二维矩阵分别表示各个像素的R、G、B三个颜色分量。每个颜色分量的数据类型一般为８位无符号整数

像素间的基本关系

一幅图像$fx,y$由基本单元像素组成，像素间存在着一定的联系，包括像素的邻域、邻接和连通，以及像素间的距离。一般地，当指定某个特定的像素时，用小写字母（如p）表示

像素的邻域

在一幅图像中，一个坐标为$x,y$的像素$p$的邻近像素组成了该像素的领域，根据邻近像素的不同定义，可以的到不同的领域，主要有4-邻域、 8-邻域以及对角邻域

4-邻域： 对于坐标为$x,y$的像素p,它有水平和垂直的4个邻近像素，记作$N_4P$
8-邻域： 对于坐标为$x,y$的像素p,包括水平、垂直和对角的８个邻近像素，记作$N_8P$
对角邻域：对于坐标为$x,y$的像素p，包括对角的3个邻近像素，记作$N_Dp$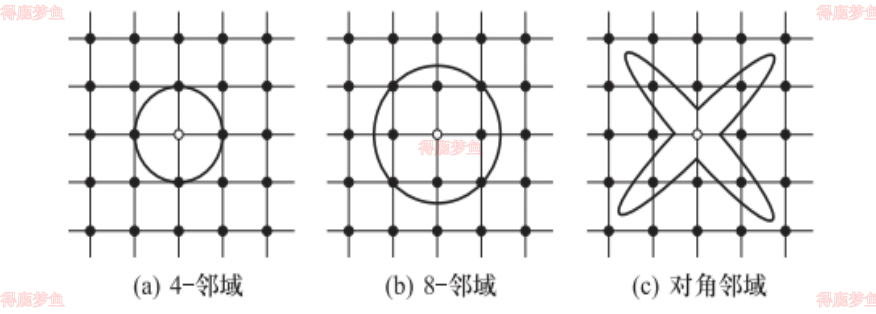

邻接与连通

对于任意的两个像素，若一个像素在另一个像素的邻域中，且它们的灰度值满足特定的相似准则（如灰度值集合），则称这两个像素是邻接的

令Ｖ表示关于邻接的灰度值集
4-邻接： 对于具有值Ｖ的像素p、q，如果ｑ在集合$N_4p$中，则称这两个像素是4-邻接
8-邻接： 对于具有值Ｖ的像素p、q，如果ｑ在集合$N_8p$中，则称这两个像素是8-邻接
m-邻接： 对于具有值Ｖ的像素p、q，如果p、q是4-邻接的，或者q在集合$N_Dp中并且在$N_4p$和$N_4q$的交集为空，则称这两个像素是m-邻接，

在介绍像素间的连通之前，先定义像素间的通路。从坐标为$x,y$的像素ｐ到坐标为$x_n,y_n的像素q的一条通路由像素序列组成，对应的坐标序列为$x_0,y_0,x_1,y_1,x_2,y_2,\cdots,x_n,y_n$,且$x_i, y_i和$x_{i+1}, y_{i+1}$是邻接的，其中$1 \leq i \leq n$,n为通路的长度。若$x_0,y_0=x_n,y_n$,则该通路是闭合通路。根据不同的邻接类型可以得到不同的通路，如４4-通路、8-通路和m-通路

像素间的距离

像素在空间上的接近程度用距离来度量。对于任意的像素p、q和r，坐标分别为$x,y,s,t,u,v$若满足
$\text{1.} Dp,q \geq 0当且仅当p=q是等号成立 \\\text{2.} Dp,q = Dq,p\\\text{3.} Dp,r \leq Dp,q + Dq,r$
则称函数Ｄ为距离或度量函数

在数字图像中，对上述距离函数Ｄ有几种不同定义，常见的有欧式距离、城区距离、棋盘距离等

欧式距离: $D_rp,q = \sqrt{x - s^2 + y - t^2}$
城区距离: $D_rp,q$ = x - s + y - t
棋盘距离: $D_rp,q$ = maxx - s, y - t