得鹿梦鱼 得鹿梦鱼
知识库 前端技能树 面试题 学习资料 关于本人

神经网络中的三个基本概念

通俗的理解三大概念

神经网络训练的基本思想就是：先“猜”一个结果，即预测结果A，看看这个预测结果和事先标记好的训练集中的真实结果Y之间的差距，然后调整策略，再试一次，这一次就不是“猜”了，而是有依据地向正确的方向靠近。如此反复多次，一直到预测结果和真实结果之间相差无几，就结束训练。

在神经网络训练中，把“猜”叫作初始化，可以随机，也可以根据以前的经验给定初始值。即使是“猜”，也是有技术含量的

神经网络中的三大概念是：反向传播，梯度下降，损失函数

例
示例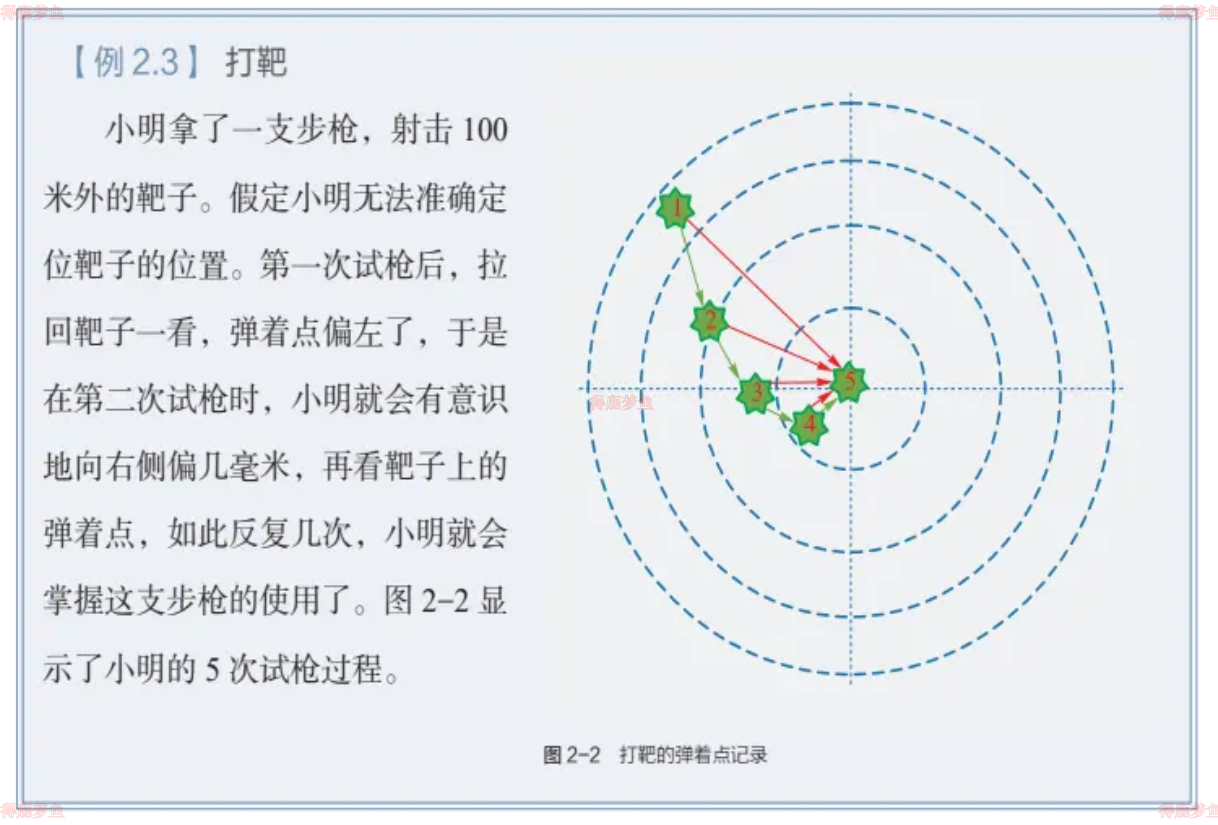

在有监督的学习中，需要衡量神经网络输出和预期的输出之间的差异大小。这种误差函数能够反映出当前网络输出和实际结果之间的不一致程度，也就是说误差函数的函数值越大，反映出模型预测的结果越不准确

在例2.3中，小明预期的目标是全部命中靶心，从最外圈至靶心各圈得分依次为1分，2分，3分，……，正中靶心可以得10分

  • 每次试枪弹着点和靶心之间的差距即为误差，可以用一个误差函数来表示，例如差距的绝对值，如图2-2中的红色线
  • 一共试枪5次，即训练（迭代）了5次
  • 每次试枪后，把靶子拉回来看弹着点，然后调整下一次的射击角度的过程，叫反向传播。注意，把靶子拉回来看和跑到靶子前面去看有本质的区别，在数学概念中，人跑到靶子前面去看，是正向微分过程；把靶子拉回来看，是反向微分过程
  • 每次调整角度的数值和方向，叫作梯度。例如向右侧调整1mm，或者向左下方调整2mm，如图2-2中的绿色矢量线
  • 图2-2是每次单发点射，所以每次训练样本的个数是1。在实际的神经网络训练中，通常需要多个样本，做批量训练，以避免单个样本本身采样时带来的误差
  • 假设一次可以连打3发子弹，每次的离散程度都类似，如果每次3发子弹连发，这3发子弹的弹着点和靶心之间的差距之和再除以3，叫作损失，可以用损失函数来表示
  • 目的：打中靶心。
  • 初始化：随便打一枪，能上靶就行，但是要记住当时的步枪的姿态。
  • 前向计算：子弹击中靶子。
  • 损失函数：环数，偏离角度。
  • 反向传播：把靶子拉回来看。
  • 梯度下降：根据本次的偏差，调整步枪的射击角度，再次进行前向计算

线性反向传播

正向计算

假设一个函数z=x⋅yz = x \cdot y其中x=2w+3bx = 2w + 3b, y=2b+1y = 2b + 1,最终的z值守变量w，b和计算式x，y的影响，常数是定值不考虑

反向传播求解w

1 求w的偏导

令w=3,b=4w =3 , b = 4则z=162z = 162,如果要使z=150z = 150, w应该如何变化，为了简化问题，暂时只考虑w的变化，令b=4b=4，如果要解决这个问题，可以在输入端不断的尝试，例如w=2试试，w=2.5等等。直到满意为止，下面讲解一个更好的解决办法：反向传播

从z开始一层一层向回看，关于变量w的偏导计算结果如下

因为z=x⋅yz = x\cdot y,其中x=2w+3bx = 2w + 3b, y=2b+1y = 2b + 1所以

∂z∂w=∂z∂x⋅∂x∂w=y⋅2=18\frac{\partial z }{\partial w} = \frac{\partial z }{\partial x} \cdot \frac{\partial x }{\partial w} = y \cdot 2 = 18

2 求w的具体变化值
∂z∂w=18\frac{\partial z }{\partial w} = 18的含义是：当w发生变化时，z的变化值是w的变化值的18倍。目的是z=150，目前在初始状态时是162，所以，问题转化为：如果需要z从162变到150时，w需要变化多少?
既然Δz=18Δw\Delta z = 18 \Delta w则Δw=118Δz\Delta w = \frac{1}{18}\Delta z
所以Δw=162−15018=0.6667,w=3−Δw=2.3333\Delta w = \frac{162 - 150}{18} = 0.6667, w = 3 - \Delta w = 2.3333
通过计算 很快就能z值变为149.9994,与150非常的接近

反向传播求解b

1 求b的偏导
∂z∂b=∂z∂x⋅∂x∂b+∂z∂y⋅∂y∂b=y⋅3+x⋅2=63\frac{\partial z }{\partial b} = \frac{\partial z }{\partial x} \cdot \frac{\partial x }{\partial b} + \frac{\partial z }{\partial y} \cdot \frac{\partial y }{\partial b} = y \cdot 3 + x \cdot 2 = 63

2 求b的具体变化值

上式的含义是：当b发生变化时，z的变化值是b的变化值的63倍。目的是让z=150，目前在初始状态时是162，所以，问题转化为z需要从162变到150时，b需要变化多少
b=4−162−15063=3.8095b = 4 -\frac{162 - 150}{63} = 3.8095

同时求解w和b的变化值

同时改变w和b，使得最终结果为z=150已知Δz=12\Delta z = 12,不妨设定w，b各贡献一半的误差z则存在
Δb=6/63=0.095,b=3.905Δw=6/18=0.333,w=2.667\Delta b = 6 / 63 = 0.095, b = 3.905 \\\Delta w = 6 / 18 = 0.333, w = 2.667

梯度下降

在自然界中，梯度下降的最好例子就是泉水流下山的过程（此处忽略泉水流动的惯性）

（1）泉水受重力影响，会在当前位置，沿着最陡峭的方向流动，有时会形成瀑布——梯度下降。
（2）泉水流下山的路径不是唯一的，在同一个地点，有可能有多个位置具有同样的陡峭程度，而造成了分流——可以得到多个解。
（3）遇到坑洼地区，有可能形成湖泊，而终止下山过程——不能得到全局最优解，而是局部最优解。

梯度下降的数学公式θn+1=θn−η⋅∇Jθ\theta_{n+1} = \theta_n - \eta \cdot \nabla J \theta
其中η\eta:学习率或步长，控制每一步走的距离，不能太快以免错过最佳景点，不能太慢以免时间太长；∇\nabla: 梯度，函数当前位置的最快上升

原文链接

神经网络中的三个基本概念
≡