单入单出的单层神经网络————单变量线性回归

单变量线性回归问题

提出问题

在互联网建设初期，各大运营商需要解决的问题就是保证服务器所在的机房的温度常年保持在23℃左右。在一个新建的机房里，如果计划部署346台服务器，应该如何配置空调的最大功率？

这个问题虽然能通过热力学计算得到公式，但是总会有误差。因此人们往往会在机房里装一个温控器，来控制空调的开关或制冷能力，风扇的转速等，其中最大制冷能力是一个关键性的数值。更先进的做法是直接把机房建在海底，用隔离的海水循环降低空气温度的方式来冷却

通过一些统计数据（称为样本数据），可以得到表。一般把自变量X称为样本特征值，把因变量Y称为样本标签值。

样本序号	服务其的数量X/千台	空调功率Y /KW
1	0.928	4.824
2	0.469	2.950
3	0.855	4.643
$\cdots$	$\cdots$	$\cdots$
这个数据是二维的，所以可以用可视化的方式来表示，结果 如下

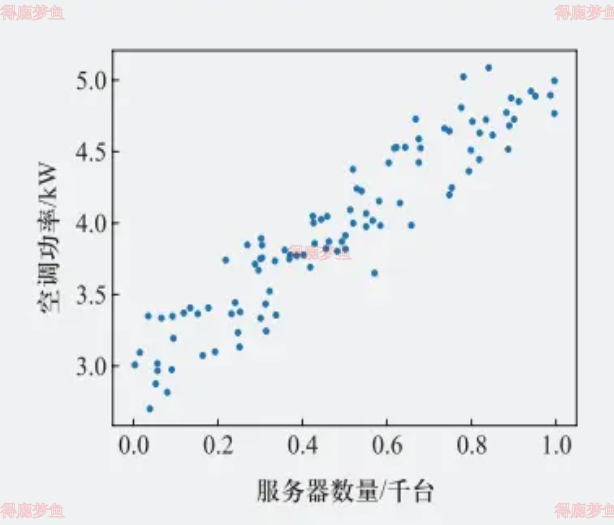通过对图的观察，可以判断它属于一个线性回归问题，而且是最简单的一元线性回归。于是，把热力学计算的问题转换成一个统计问题，因为不能精确地计算出每块电路板或每台机器到底能产生多少热量。
部分读者可能会想到一个办法：在样本数据中，找一个与346非常近似的例子，以它为参考就可以找到合适的空调功率数值
当然，这样做是完全科学合理的，实际上这就是线性回归的解题思路：利用已有数值，预测未来值。也就是说，这些读者不经意间使用了线性回归模型。

一元线性回归模型

回归分析是一种数学模型。当因变量和自变量为线性关系时，它是一种特殊的线性模型。

最简单的情形是一元线性回归，有大体上有线性关系的一个因变量和一个自变量组成，模型是$$Y=a + bX + \varepsilon$$
$X$是自变量，$Y$是因变量，$\varepsilon$是随机误差，$a$和$b$是参数，在线性回归模型中，$a$和$b$是通过算法学习出来的

从常规概念上讲，模型是人们通过主观意识借助实体或者虚拟表现来构成对客观事物的描述，这种描述通常是有一定的逻辑或者数学含义的抽象表达方式。例如对小轿车建模的话，会是这样描述：由发动机驱动的四轮铁壳子。对能量概念建模的话，那就是爱因斯坦狭义相对论的著名推论：$E = mc^2$

对数据建模的话，就是用一个或几个公式来描述这些数据的产生条件或者相互关系，例如有一组数据是大致满足$y=3x+2$这个公式，那么这个公式就是模型。为什么说是“大致”呢？因为在现实世界中，一般都有噪声（误差）存在，所以不可能非常准确地满足这个公式，只要是在这条直线两侧附近，就可以算作是满足条件

对于线性回归模型，有如下几点需要了解

• 通常假定随机误差的均值是0,方差为$\sigma^2$
• 进一步假定随机误差遵从正态分布，就叫正态线性模型
• 一般地，若有k个自变量和1个因变量，则因变量的值分为两部分：一部分由自变量影响，即表示为他的函数，另一部分优其他的未考虑因素和随机影响，即随机误差

当函数为参数未知的线性函数时，称为线性回归分析模型。
当函数为参数未知的非线性函数时，称为非线性回归分析模型。
当自变量个数大于1时称为多元回归。
当因变量个数大于1时称为多重回归

公式形式

$$\bm{Y} = \bm{X} \cdot \bm{W} + \bm{B} = \begin {bmatrix} x_1 & x_2 & x_3\end{bmatrix}\begin {bmatrix} w_1 \\w_2 \\w_3\end{bmatrix}\text{+}b$$

最小二乘法

最小二乘法，也叫最小平方法（least square method），它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和最小。最小二乘法还可用于曲线拟合。其他优化问题，如通过最小化能量或最大化熵，也可用最小二乘法来表达

2数学原理

线性回归试图学习$zx_i = w \cdot x_i + b$使得$zx_i \approx{} y_i$,其中$x_i$是样本特征值，$y_i$是样本标签值，$zx_i$是模型的预测值

$$J = \sum_{i=0}^{m-1}zx_i - y_i^2 = \sum_{i=0}^{m-1}y_i - wx_i -b^2$$
J为损失函数。实际上就是试图找到一条直线，使所有样本到直线上的残差的平方和最小。

如果想让误差的值最小，通过对w和b求导，再令导数为0，就是w和b的最优解。推导过程如下
$$\frac{\partial J}{\partial w} = \frac{\partial \left \{ \sum_{i=1}^my_i - wx_i -b^2 \right \} }{\partial w } = 2 \sum_{i=1}^my_i - wx_i -b-x_i$$
令上式为0，则有
$$\sum_{i=1}^my_i - wx_i -bx_i = 0 \tag{1}$$
$$\frac{\partial J}{\partial b} = \frac{\partial \left \{ \sum_{i=1}^my_i - wx_i -b^2 \right \} }{\partial b } = 2 \sum_{i=1}^my_i - wx_i -b-1$$
令上式为0，则有
$$\sum_{i=1}^my_i - wx_i -b = 0$$
由上式的
$$\sum_{i=1}^mb = m \cdot b = \sum_{i=1}^my_i - \sum_{i=1}^mx_i$$
$$b = \frac{1}{m}\left \{ \sum_{i=1}^my_i - \sum_{i=1}^mx_i \right \} = \bar y - w\bar x \tag{2}$$

将2代入1中
$$\sum_{i=1}^my_i - wx_i -bx_i = \sum_{i=1}^my_i - wx_i - \bar y + w\bar x x_i = 0$$

$$= \sum_{i=1}^mx_iy_i - wx_i^2 - \bar yx_i + w\bar x x_i = 0$$

$$\sum_{i=1}^mx_iy_i - x_i\bar y - w\sum_{i=1}^mx_i^2 - \bar x x_i = 0$$

$$w = \frac{\sum_{i=1}^mx_iy_i - x_i\bar y}{\sum_{i=1}^mx_i^2 - \bar x x_i} \tag{3}$$

梯度下降

数学原理

在下面的公式中，规定$x_i$是第$i$个样本特征值（单特征），$y_i$是第$i$个样本标签值，$z_i$是第$i$个预测值

预设函数（hypothesis function）为一个线性函数$z_i = x_i \cdot w + b$

损失函数为均方差函数 $lossw,b = \frac{1}{2}z_i - y_i^2$

与最小二乘法相比，梯度下降法和最小二乘法的模型及损失函数是相同的，都是线性模型加均方差损失函数。模型用于拟合，损失函数用于评估效果。区别在于，最小二乘法从损失函数求导，直接求得数学解析解，而梯度下降法以及后面的神经网络法，都是利用导数传递误差，再通过迭代的方式用近似解逼近真实解

梯度计算

1 计算z的梯度

$$\frac{\partial loss}{\partial z_i} = z_i - y_i$$

2 计算w的梯度

$$\frac{\partial loss}{\partial w} = \frac{\partial loss}{\partial z_i}\frac{\partial z_i}{\partial w} = z_i - y_ix_i$$

2 计算b的梯度

$$\frac{\partial loss}{\partial b} = \frac{\partial loss}{\partial z_i}\frac{\partial z_i}{\partial b} = z_i - y_i$$

神经网络法

定义神经网络结构

首次尝试建立神经网络，先用一个最简单的单层单点神经。

输入层此神经元在输入层只接受一个输入特征，经过参数w，b的计算后，直接输出结果。这样一个简单的“网络”，只能解决简单的一元线性回归问题，而且由于是线性的，不需要定义激活函数，大大简化了程序。
权重w和b因为是一元线性问题，所以w和b都是一个标量
输出层输出层为1个神经元，线性预测公式$z_i = wx_i +b$
损失函数使用均方差函数 $lossw,b = \frac{1}{2}z_i - y_i^2$

反向传播

2 计算w的梯度

$$\frac{\partial loss}{\partial w} = \frac{\partial loss}{\partial z_i}\frac{\partial z_i}{\partial w} = z_i - y_ix_i$$

2 计算b的梯度
$$\frac{\partial loss}{\partial b} = \frac{\partial loss}{\partial z_i}\frac{\partial z_i}{\partial b} = z_i - y_i$$

梯度下降的三种形式

单样本随机梯度下降

训练样本：每次使用一个样本数据进行一次训练，更新一次梯度，重复以上过程。
优点：训练开始时损失值下降很快，随机性大，找到最优解的可能性
缺点：受单个样本的影响大，损失函数值波动大，到后期徘徊不前，在最优解附近震荡；不能并行计算。

小批量样本梯度下降

训练样本：选择一小部分样本进行训练，更新一次梯度，然后再选取另外一小部分样本进行训练，再更新一次梯度。
优点：不受单样本噪声影响，训练速度较快。
缺点：批大小的选择很关键，会影响训练结果

全批量样本梯度下

训练样本：每次使用全部数据集进行一次训练，更新一次梯度，重复以上过程。
优点：受单个样本的影响最小，一次计算全体样本速度快，损失函数值没有波动，到达最优点平稳，方便并行计算。
缺点：数据量较大时不能实现（内存限制），训练过程变慢。初始值不同，可能导致获得局部最优解，并非全局最优解

原文链接