多入单出的单层神经网络——多变量线性回归

提出问题

问题：在北京通州，距离通州区中心15km的一套93m2的房子，大概是多少钱

房价预测问题，是机器学习的一个入门话题。影响北京通州房价的因素有很多，居住面积、地理位置、朝向、学区房、周边设施、建筑年份等，其中，面积和地理位置是两个比较重要的因素。地理位置信息一般采用经纬度方式表示，但是经纬度是两个特征值，联合起来才有意义，因此，本章中把它转换成了到通州区中心的距离

样本数据如下

特征值1地理位置 最大值 21.96km 最小值 2.02km 平均值 12.13km
特征值2居住面积 最大值 119 最小值 40 平均值 78.9
特征值3价格 最大值 674.37 最小值 181.38 平均值 420.64

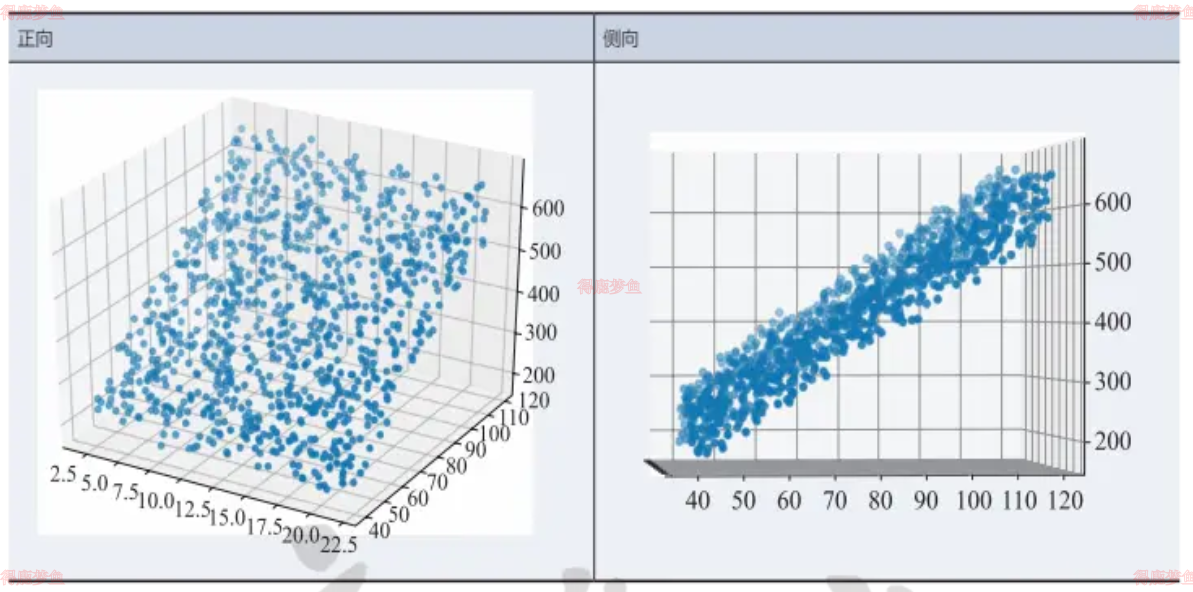
从正向看，很像一块草坪，似乎是一个平面。再从侧向看，和第4章中的直线拟合数据很像。所以，对于这种三维的线性拟合，可以把它想象成为拟合一个平面，这个平面会位于这块“草坪”的中位，把“草坪”分割成上下两块更薄的“草坪”，最终使得所有样本点到这个平面的距离的平方和最小

多元线性回归模型

由于表中可能没有恰好符合15km、$93m^2$条件的数据，因此需要根据1000个样本值来建立一个模型，来解决预测问题

通过图示，基本可以确定这个问题是个线性回归问题，而且是典型的多元线性回归，即包括两个或两个以上自变量的回归。多元线性回归的函数模型

$y = a_0x_0 + a_ix_i + \cdots + a_nx_n + b$

对于一般的应用问题，建立多元线性回归模型时，为了保证回归模型具有优良的解释能力和预测效果，应首先注意自变量的选择，准则如下

1. 自变量对因变量必须要有显著的影响，并且呈现密切的线性相关
2. 自变量与因变量之间的线性相关必须是真实的
3. 自变量之间应具有一定的互斥性，即自变量之间的相关程度不应高于自变量与因变量之间的相关程度。
4. 自变量应具有完整的统计数据，其预测值容易确定

解决方案

正规方程解法

对于线性回归问题，除了前面提到的最小二乘法可以解决一元线性回归的问题外，也可以解决多元线性回归问题
对于多元线性回归，可以用正规方程（normalequation）来解决，也就是得到一个数学上的解析解，又叫解方程法。具体的公式描述如下
$y = a_0x_0 + a_ix_i + \cdots + a_nx_n + b$

简单的推导方法

在做函数拟合（回归）时预设函数h为
$hw,b = w_0x_0 + w_ix_i + \cdots + w_nx_n + b$
令$b = w_0$
$hw,b = w_0x_0 + w_ix_i + \cdots + w_nx_n + w_0$

如果把m个样本一起计算，将会得到如下矩阵。

$\bm{H} = \bm{X} \cdot \bm{W}$

$$\bm{X} = \begin {bmatrix}1 & x_{1,1} & x_{1,2} \\1 & x_{2,1} & x_{2,2} \\\vdots & \vdots & \vdots \\1 & x_{m,1} & x_{m,2} \end{bmatrix}$$

$$\bm{W} = \begin {bmatrix}w_1 &w_2 &\vdots &w_m\end{bmatrix}$$

$$\bm{Y} = \begin {bmatrix}y_1 \\y_2 \\\vdots \\y_m\end{bmatrix}$$

直观上看，$\bm W=\bm Y/ \bm X$，但是这里三个值都是矩阵，而矩阵没有除法，所以需要得到X的逆矩阵，用$\bm Y$乘以$\bm X$的逆矩阵即可。但是又会遇到一个问题，只有方阵才有逆矩阵，而$\bm X$不一定是方阵，所以要先把左侧变成方阵，就可能会有逆矩阵存在了。所以，先把等式两边同时乘以$\bm X$的转置矩阵$\bm X^T$\bm，以便得到$\bm X$的方阵$\bm X^T \bm X \bm W = \bm X^T \bm Y$

$\bm X^T \bm X$一定是个方阵，并且假设其存在逆矩阵，把它移到等式右侧$\bm W = \bm X^T \bm X^{-1}\bm X^T \bm Y$

复杂的推导方法

损失函数为均方差函数 $lossw,b = \sumz_i - y_i^2$
把b看作是一个恒等于1的特征，并把$\bm{Z} = \bm{XW}$代入
$$J = \sumx_iw_i - y_i^2 = \bm{XW - Y}^T \cdot \bm{XW - Y}$$

对$w_i$求导，令导数为0，就是$w_i$的最小值解
$$\frac{\partial JW}{\partial w_i} = \frac{\partial}{\partial w_i}\left [\bm{XW - Y}^T \cdot \bm{XW - Y} \right ] \\= \frac{\partial}{\partial w_i}\left [\bm{X^TW^T - Y^T} \cdot \bm{XW - Y} \right ] \\= \frac{\partial}{\partial w_i}\left [\bm{X^TXW^TW - X^TW^TY - Y^TXW + Y^TY} \right ]$$

求导后第一项为$2\bm{X^TXW}$,第二项和第三项都为$\bm{X^TY}$第四项的结果为0，在令导数为0，
$$J'w = 2\bm{X^TXW} - 2\bm{X^TY} = 0$$
$$\bm{W} = \bm{X^TX}^{-1} \bm{X}^T\bm{Y}$$
逆矩阵$\bm{X^TX}^{-1}$可能不存在的原因
（1）特征值冗余，例如$x_2 = x_1^2$，即正方形的边长与面积的关系，不能作为两个特征同时存在。
（2）特征数量过多，例如特征数n比样本数m还要大

神经网络法

多变量（多特征值）的线性回归可以看作是一种高维空间的线性拟合。以具有两个特征值的情况为例，这种线性拟合不再用直线去拟合点，而是用平面去拟合点

定义神经网络结构

• 没有中间层，只有输入项和输出层（输入项不算一层）
• 输出层只有一个神经元
• 神经元有一个线性输出，不经过激活函数处理

归一化

把数据线性地变成[0,1]或[-1,1]之间的小数，把带单位的数据（如米，千克等）变成无量纲的数据，区间缩放。归一化有三种方法

min-max归一化
$$x_{new} = \frac{x - x_{min}}{x_{max} - x_{min} }$$
均值归一化
$$x_{new} = \frac{x - \bar{x}}{x_{max} - x_{min} }$$
非线性归一化

• 对数转换
  $$y = logx$$
• 反余切转换

$$y = arccotx \cdot 2/ \pi$$

标准化

把每个特征值中的所有数据，变成平均值为0，标准差为1的数据，最后为正态分布。Z-score规范化也叫标准差标准化或零均值标准化，其中std是标准差
$$x_{new} = x - \bar{x} /std$$

中心化

平均值为0，无标准差要求
$$x_{new} = x - \bar{x}$$

原文链接