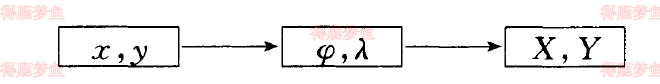空间数据的变换算法 平面坐标变换 平面直角坐标系的建立 在平面上选一点O O O O O O
平面坐标变换矩阵 T = [ a d g b e h c f i ] \text{T}=\left [\begin{matrix}a & d & g \\b & e & h \\c & f & i\end{matrix}\right ] T = a b c d e f g h i
从变化功能上可以吧T T T T 1 = [ a d b e ] 对图形进行缩放、旋转、对称、错切 T_1=\left [\begin{matrix}a & d \\ b & e \end{matrix}\right ]\text{对图形进行缩放、旋转、对称、错切} T 1 = [ a b d e ] 对图形进行缩放、旋转、对称、错切 T 2 = [ c f ] 对图形进行平移 T_2=\left [\begin{matrix}c & f \end{matrix}\right ]\text{对图形进行平移} T 2 = [ c f ] 对图形进行平移 T 3 = [ g h ] 对图形进行投影变换 T_3=\left [\begin{matrix}g \\h\end{matrix}\right ]\text{对图形进行投影变换} T 3 = [ g h ] 对图形进行投影变换 T 3 = [ i ] 对图形进行整体缩放 T_3=\left [\begin{matrix}i\end{matrix}\right ]\text{对图形进行整体缩放} T 3 = [ i ] 对图形进行整体缩放
平移变换 [ x ∗ y ∗ 1 ] = [ x y 1 ] × [ 1 0 0 0 1 0 T x T y 1 ] = [ x + T x y + T y 1 ] \left [\begin{matrix}x^* & y^* & 1\end{matrix}\right ] \text{=}\left [\begin{matrix}x & y & 1\end{matrix}\right ]\times\left [\begin{matrix}1 & 0 & 0 \\0 & 1 & 0 \\T_x & T_y & 1 \end{matrix}\right ]\text{=}\left [\begin{matrix}x + T_x & y + T_y & 1\end{matrix}\right ] [ x ∗ y ∗ 1 ] = [ x y 1 ] × 1 0 T x 0 1 T y 0 0 1 = [ x + T x y + T y 1 ]
比例变换 [ x ∗ y ∗ 1 ] = [ x y 1 ] × [ S x 0 0 0 S y 0 0 0 1 ] = [ x × S x y × S y 1 ] \left [\begin{matrix}x^* & y^* & 1 \end{matrix}\right ] \text{=}\left [\begin{matrix}x & y & 1 \end{matrix}\right ]\times\left [\begin{matrix}S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{matrix}\right ]\text{=}\left [\begin{matrix}x \times S_x & y \times S_y & 1 \end{matrix}\right ] [ x ∗ y ∗ 1 ] = [ x y 1 ] × S x 0 0 0 S y 0 0 0 1 = [ x × S x y × S y 1 ]
对称变换 [ x ∗ y ∗ 1 ] = [ x y 1 ] × [ a d 0 b e 0 0 0 1 ] = [ a x + b y d x + e y 1 ] \left [\begin{matrix}x^* & y^* & 1 \end{matrix}\right ] \text{=}\left [\begin{matrix}x & y & 1 \end{matrix}\right ]\times\left [\begin{matrix}a & d & 0 \\ b & e & 0 \\ 0 & 0 & 1 \end{matrix}\right ]\text{=}\left [\begin{matrix}ax + by & dx + ey & 1 \end{matrix}\right ] [ x ∗ y ∗ 1 ] = [ x y 1 ] × a b 0 d e 0 0 0 1 = [ a x + b y d x + ey 1 ]
旋转变换 [ x ∗ y ∗ 1 ] = [ x y 1 ] × [ cos θ sin θ 0 − sin θ cos θ 0 0 0 1 ] = [ x cos θ − y sin θ x sin θ + y cos θ 1 ] \left [\begin{matrix}x^* & y^* & 1 \end{matrix}\right ] \text{=}\left [\begin{matrix}x & y & 1 \end{matrix}\right ]\times\left [\begin{matrix}\cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix}\right ]\text{=}\left [\begin{matrix}x\cos\theta - y\sin\theta & x\sin\theta + y\cos\theta & 1 \end{matrix}\right ] [ x ∗ y ∗ 1 ] = [ x y 1 ] × cos θ − sin θ 0 sin θ cos θ 0 0 0 1 = [ x cos θ − y sin θ x sin θ + y cos θ 1 ]
错切变换 [ x ∗ y ∗ 1 ] = [ x y 1 ] × [ 1 d 0 b 1 0 0 0 1 ] = [ x + b y d x + y 1 ] \left [\begin{matrix}x^* & y^* & 1 \end{matrix}\right ] \text{=}\left [\begin{matrix}x & y & 1 \end{matrix}\right ]\times\left [\begin{matrix}1 & d & 0 \\ b & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right ]\text{=}\left [\begin{matrix}x + by & dx + y & 1\end{matrix}\right ] [ x ∗ y ∗ 1 ] = [ x y 1 ] × 1 b 0 d 1 0 0 0 1 = [ x + b y d x + y 1 ]
复合变换 复合变换是指图形做一次以上的几何变换,变换结果是每次变换矩阵相乘
注意 平移变换值改变图形的位置,不改变图形的大小和形状
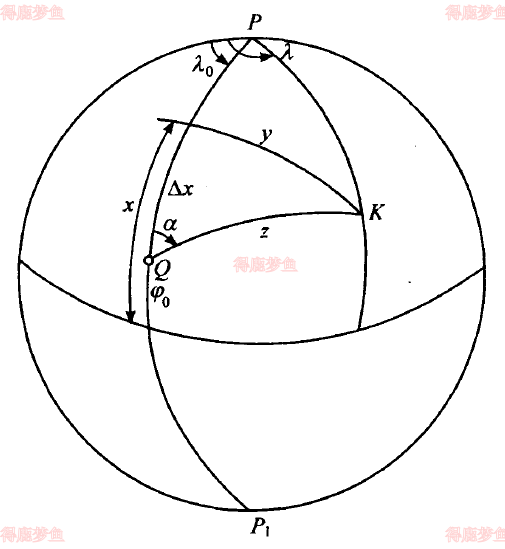
球面坐标变换 球面坐标系的建立 为在球面上确定点位可视需要而采用不同的坐标系,实践中常使用的有地理坐标系φ , λ \varphi,\lambda φ , λ a , z a,z a , z x , y x,y x , y
地理坐标与球面极坐标之间的关系{ cos z = sin φ sin φ 0 + cos φ cos φ 0 cos λ − λ 0 sin z cos a = sin φ cos φ 0 − cos φ sin φ 0 cos λ − λ 0 sin z sin a = cos φ sin λ − λ 0 \begin{cases}\cos z = \sin\varphi\sin{\varphi_0} + \cos\varphi\cos{\varphi_0}\cos\lambda - {\lambda_0}\\\sin z \cos a =\sin\varphi\cos{\varphi_0} - \cos\varphi\sin{\varphi_0}\cos\lambda - {\lambda_0}\\\sin z \sin a = \cos\varphi\sin\lambda - {\lambda_0}\end{cases} ⎩ ⎨ ⎧ cos z = sin φ sin φ 0 + cos φ cos φ 0 cos λ − λ 0 sin z cos a = sin φ cos φ 0 − cos φ sin φ 0 cos λ − λ 0 sin z sin a = cos φ sin λ − λ 0 φ 0 , λ 0 {\varphi_0},{\lambda_0} φ 0 , λ 0
球面直角坐标与球面极坐标的关系{ cot a = sin △ x cot y cos z = cos △ x cot y △ x = x − φ 0 \begin{cases}\cot a = \sin\triangle{x}\cot{y}\\\cos z = \cos\triangle{x}\cot{y} \\\triangle{x} = x - {\varphi_0}\end{cases} ⎩ ⎨ ⎧ cot a = sin △ x cot y cos z = cos △ x cot y △ x = x − φ 0
在采用球面级坐标系时,首先要确定一个极坐标的“极点”Q,球面上的各点便可以以新级Q为原点,以方位角α \alpha α z z z α \alpha α λ \lambda λ 90 ∘ − φ 90^{\circ} - \varphi 9 0 ∘ − φ
确定新极Q地理坐标中的φ 0 , λ 0 {\varphi_0},{\lambda_0} φ 0 , λ 0 通常可按照已有的数据确定Q点以及φ 0 , λ 0 {\varphi_0},{\lambda_0} φ 0 , λ 0 { φ 0 = 1 n ∑ i = 1 n φ i λ 0 = 1 n ∑ i = 1 n λ i \begin{cases}{\varphi_0} = \frac{1}{n} \sum_{i=1}^n {\varphi_i} \\{\lambda_0} = \frac{1}{n} \sum_{i=1}^n {\lambda_i}\end{cases} { φ 0 = n 1 ∑ i = 1 n φ i λ 0 = n 1 ∑ i = 1 n λ i
新极通过投影区域中部大圆的天顶 新极通过投影区域中部小圆的天顶 仿射变换 仿射变换是使用最多的一种几何纠正方式。在保留线条平行条件下。仿射转换允许对长方形目标做旋转、平移、倾斜和不均匀缩放。
底图投影变换 概述 当系统所使用的数据是来自不同地图投影的图幅时,需要将一种投影的几何数据转换成所需投影的几何数据,这就需要进行地图投影变换。{ X = f 1 x , y Y = f 2 x , y \begin{cases}X = f_1x,y \\Y = f_2x,y\end{cases} { X = f 1 x , y Y = f 2 x , y
反解变换法 是一种中间过渡的方法,即先解出原地图投影点的地理坐标,将其带入新图的投影公式求的坐标
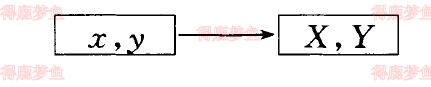
正解变换法 不需要反解出原地图投影点的地理坐标的解析公式,而是直接求出两种投影点的直角坐标关系式
如果原投影点的坐标解析式不知道,或者不易求出两投影之间坐标的直接关系,可以采用多项式逼近的方式,即用数值变换法来建立两投影间的变换公式;例如可以采用二元三次多项式进行变换{ X = a 00 + a 10 x + a 01 y + a 20 x 2 + a 11 x y + a 02 y 2 + a 30 x 2 + a 21 x 2 y + a 12 x y 2 + a 03 y 3 Y = b 00 + b 10 x + b 01 y + b 20 x 2 + b 11 x y + b 02 y 2 + b 30 x 2 + b 21 x 2 y + b 12 x y 2 + b 03 y 3 \begin{cases}X = a_{00} + a_{10}x + a_{01}y + a_{20}x^2 + a_{11}xy + a_{02}y^2 + a_{30}x^2 + a_{21}x^2y + a_{12}xy^2 + a_{03}y^3 \\Y = b_{00} + b_{10}x + b_{01}y + b_{20}x^2 + b_{11}xy + b_{02}y^2 + b_{30}x^2 + b_{21}x^2y + b_{12}xy^2 + b_{03}y^3\end{cases} { X = a 00 + a 10 x + a 01 y + a 20 x 2 + a 11 x y + a 02 y 2 + a 30 x 2 + a 21 x 2 y + a 12 x y 2 + a 03 y 3 Y = b 00 + b 10 x + b 01 y + b 20 x 2 + b 11 x y + b 02 y 2 + b 30 x 2 + b 21 x 2 y + b 12 x y 2 + b 03 y 3 { X = ∑ i = 1 n X i − X ′ i 2 = m i n Y = ∑ i = 1 n Y i − Y ′ i 2 = m i n \begin{cases}X = \sum_{i=1}^n {X_i - {X'}_i}^2 = min \\Y = \sum_{i=1}^n {Y_i - {Y'}_i}^2 = min\end{cases} { X = ∑ i = 1 n X i − X ′ i 2 = min Y = ∑ i = 1 n Y i − Y ′ i 2 = min n 为点数 , X i , Y i 为实际变换值 , X ′ i , Y ′ i 为理论值 n为点数, X_i, Y_i为实际变换值, {X'}_i, {Y'}_i为理论值 n 为点数 , X i , Y i 为实际变换值 , X ′ i , Y ′ i 为理论值
数值解析变换法 当已知新投影的公式,但不知原投影的公式时,可先通过数值变换求出原投影的地理坐标,然后带入新投影公式,求出新投影点的坐标
兰伯特投影 兰伯特等角投影 角度没有变形 两条标准纬线上没有任何变形 等变形线和纬线一致,即同一条纬线上的变形处处相等 在同一经线上,两标准纬线外侧为正方形,而两标准纬线之间为负变形 同一纬线上等经差的线段长度相等,两条纬线间的经线长度处处相等 墨卡托投影 是一种“等角正切圆柱投影”,假设地球被围在一中空的圆柱里,其标准纬线和圆柱相切接触,然后在假想地球中心有一盏灯,把球面上的圆形投影都圆柱体上,在吧圆柱体展开
墨卡托投影没有角度变形,由每一点向个方向的长度比相等,它的经纬线都是平行直接,且相交称为直角,经线间隔相等,纬线间隔从标准纬线向两级逐渐增大,墨卡托投影的地图上的长度和面积变形明显,但标准纬线无变形,从标准纬线向两级变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置的正确
高斯-克吕格投影 是一种“等角横切圆柱投影”,假想有一个椭圆柱套在地球椭球体的外面,并与某一子午线(中央子午线)相切,椭圆柱的中心轴位于椭球的赤道上,将中央经线东西各一定的经差范围内的经纬线交点投影到椭圆柱面上,并将此圆柱展开为平面,即得本投影
通用横轴墨卡托投影 一种“横轴等角割圆柱投影”