概述
地图符号发展至今。普通地图尤其是地形图符号。已逐渐形成为一个较为科学系统的体系
传统地图学吧地图符号的结构概括为图形、大小和色彩3个要素,随着现代科学技术的发展。吧这些要素作为地图符号的基本构成已是恨不完善的。符号视觉变量是从地图感受论引出的。
地图符号构成元素组成
地图符号的基本图形要素可以称为符号构成要素SCEsymbolic costitution elements
地图符号构成元素即组成一切符号的基本因素,是地图上最小的图解单元。它有八大元素组成:位置Pposition、形状Ffrom、色彩Hhue、尺寸Ssize、网纹Ttexture、方向Ddirection、注记Nnotation、行为Aaction
P 指符号在图上的定位。平面位置有x,y坐标标定。
F 指符号不同于外形所组成的图形特征
H 表示符号的色相H1、纯度H2和亮度H3
S 表示符号的大小S1、粗细S2、长短S3、分割比例S4
T 表示构成符号的晕点、晕线、花纹的排列和稀疏变化特征
D 表示符号的方向
N 指地图上的文字、数字和字体、字级
A 符号在不同状态下的行为和表现形式
地图符号的几何特征
根据面向对象的观点。为使各类符号对象就有相对独立性,需先将点符号、线符号、面符号定义成三种符号对象类,并将各类符号的数据成员(属性数据)及其函数成员(操作方法)封装在各自的对象类中。然后在这3个对象类的基础上。概括出更高层次的超类、即符号类
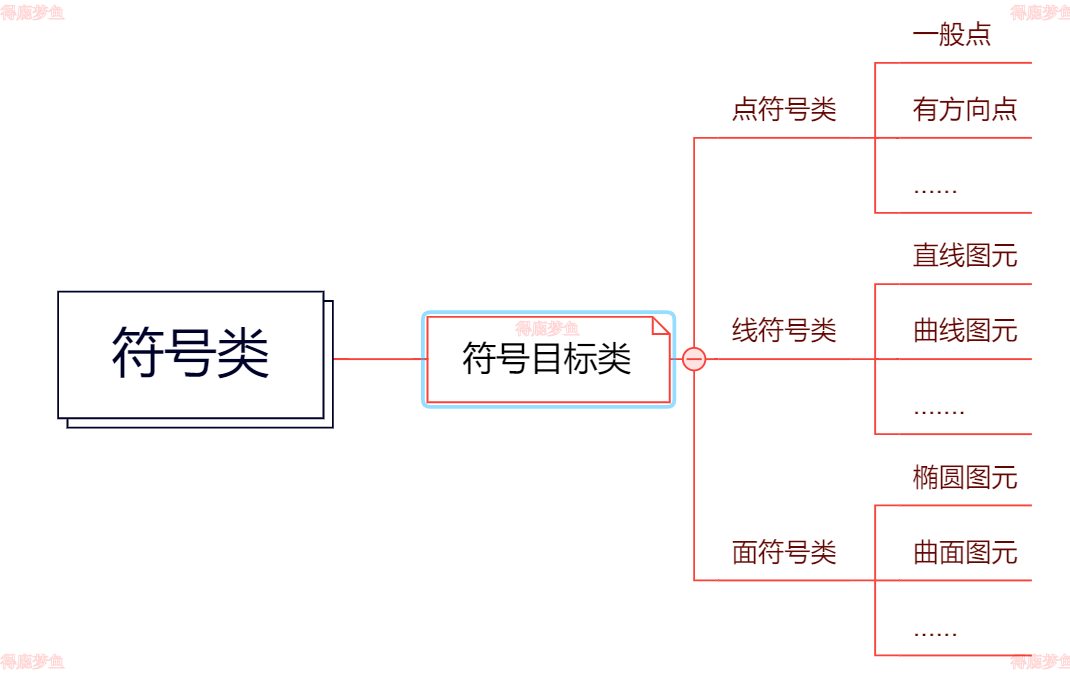
基于svg的地图符号描述模型
地图符号的描述方法可分为文字、数学方法、半结构数据模型、XML、GML、SVG描述等阶段
SVG能描述任意复杂的图形,可以应用于复杂地图符号的描述格式
SVG的主要对象可归为基本要素对象和描述对象2个大类。
基本要素对象不仅支持文字、图像和基本图形,而且对于贝塞尔曲线也同样支持,并引入路径的概念。
描述功能主要包括字体描述、坐标变换、填充、透明、链接、描边、动画、显示方式、剪切路径、组合对象及箭头等
基于SVG的地图符号描述模型包括概念模型、逻辑模型和物理模型。
概念模型
- 地图符号标记表示地图数据
- SVG标记表示地图符号
逻辑模型
SVG标记地图符号具体表现为地图符号由图形按照一定的描述规则构成和用SVG标记图形格式2部分
根据底图符号的结构特征和实现机制。在地图符号和基本图形之间插入中间件--模型,构成了地图符号描述的物理模型
一个完整的地图符号描述应该满足一下要求
- 能充分表达地图符号的几何形状
- 能方便的定义地图符号的专题属性且易于扩充
- 能方便的定义地图符号和外界的交互功能
- 能够对地图符号的几何形状和专题属性进行存取和显示。
点状地图符号绘制
点状符号可以理解为有一个模板且仅有使用一次仅排列或变形而成的
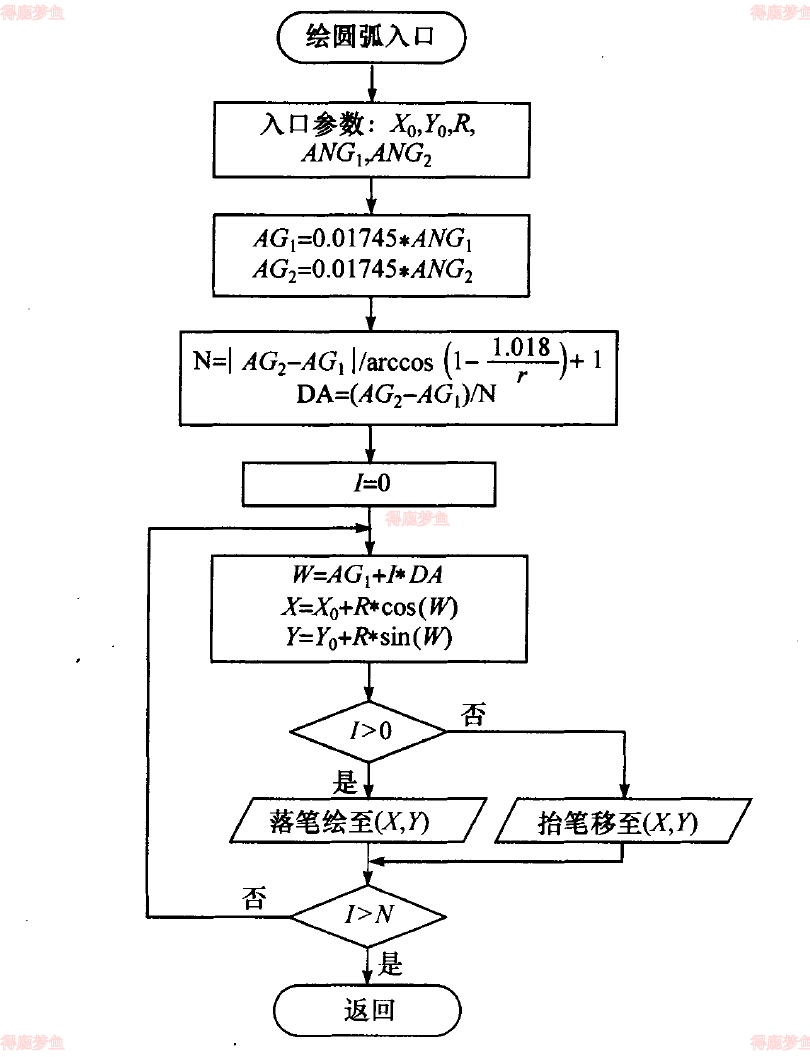
圆的绘制
圆在底图上常作为定位分级符号,器圆心定位在要素的中心位置,圆的面积表示响应的数量指标。
圆是由正多边形逼近的,当多边形的边数多到人眼分辨不出是多边形时,就形成了圆形,显然,当边数不够时就不像圆形。但如边数过多,就会使计算和输出量增加。解决的办法就是:考虑逼近圆的多边形撒花姑娘任意相邻三个顶点构成的等腰三角形的高度H,控制H在一定的限度,以致人眼分辨不出三点连线是折线。如图所示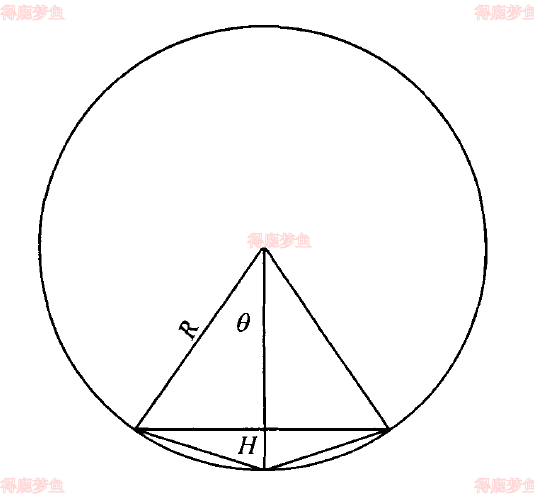
设圆的半径为R,多边形的等分角度为θ 显然H=R−Rcosθ则θ=arccos1−RH这里一般H控制在0.01~0.03之间比较适宜。
{X=X0+Rcos˙αY=Y0+Rsin˙α
X0,Y0为圆心坐标,α从圆弧的起始角ang1以增量θ变化到终止角ang2,约定当终止角大于起始角按逆时针绘制,否则按照顺时针绘制。
椭圆的绘制
椭圆由于具有长抽和短轴,它可以同时表示一种现象的2个数量指标。
椭圆也是有多边形逼近而形成的。其绘制方法同圆弧绘制相似;
椭圆的绘图参数为中心坐标X0,Y0,横半轴长度、纵半轴长度、横轴与X轴的夹角ang0,椭圆弧的起止角度ang1和ang2
逼近椭圆的多边形等分角为θ为
θ=arccos1−RHR={a2/bb2/aa>bb>a{X=X0+acosαY=Y0+bsinα
多边形的绘制
正多边形是常用的几何符号,地图上有很多符号是由三角形、方形、五角星等正多边形构成的。
设多边形的外接圆中心坐标为X0,Y0, 半径为R,边数为N,底边和X轴夹角为α
等分角θ=N2π
底边左端点的起始角为W0=α+2π+θ
ParseError: KaTeX parse error: Undefined control sequence: \cosW at position 26: …es}X = X_0 + R\̲c̲o̲s̲W̲ ̲\\Y = Y_0 + R\…
五角星的绘制
绘制五角星的参数为中心坐标X0,Y0,外接圆的半径R,由于五角星的1讴歌顶点等分整个圆周角,所以两个相邻点的和中心连线的夹角都是5π
内接圆的半径R'
由图14.9中A和B两点的Y坐标相等得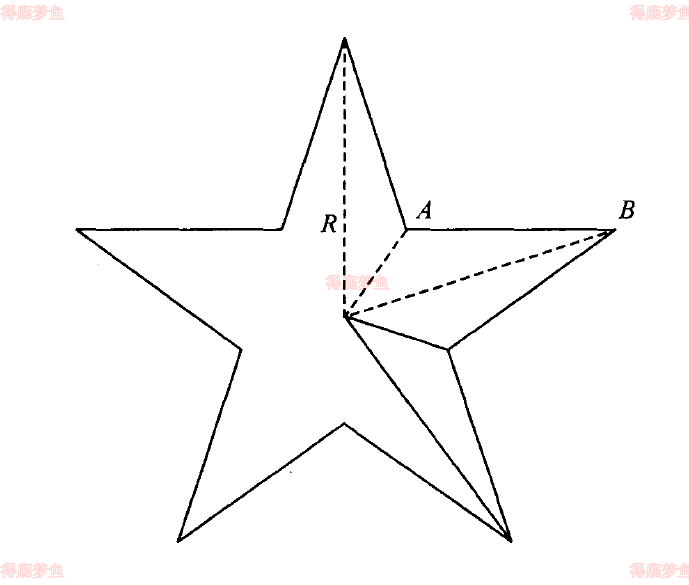
R′sin2π−5π=Rsin2π−52πRR′=cos5πcos52π≈0.38196602
线状地图符号绘制
线状符号的设计是一个较为复杂的过程。将符号的基本信息描述为模板,再把模板在中轴线上分段串接并作为相应的变形处理,尤其是拐弯处。取线状符号的基本最小循环单位作为模板中的主要图元的描述,求出外接矩形,作为模板串接或者变形时参与运算的图元的有效范围,按模板的长度在中轴线上分段截取,若模板超出拐点则将截取超出部分,截取部分转到下一折线段内处理。对有截取部分的模板实行从矩形到四边形的变形处理
平行线绘制
平行线是由2条距离相等的平行曲线构成的,通常用于表示道路等地物。设平行线的绘图参数为定位曲线坐标xi,yi,i=1,2,3...;平行线宽W
曲线是由一系列的直线构成的。绘制平行线就是绘制定位曲线各直线段2侧的平行线段组成的2条曲线。为了提高绘图速度。采用对平行的2条曲线相互反向绘制的方式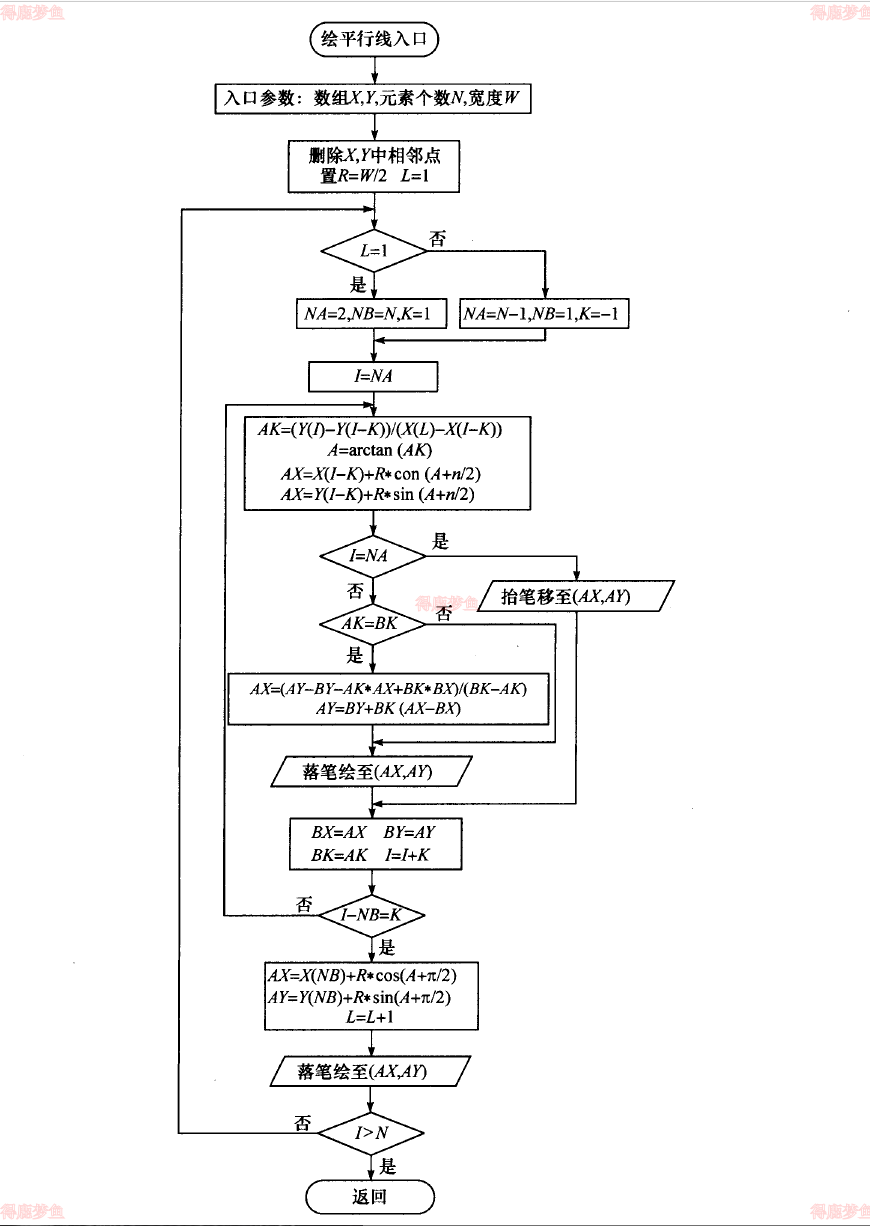
虚线绘制
虚线是由一系列相间排列的等长短线段构成的。虚线亦称间断线。地图上常用虚线绘制大桥、等高线的间曲线等地形地物。
设虚线的的绘图参数:定位曲线的坐标和坐标个数,虚线段的长度DIS1,虚线段的间距DIS2
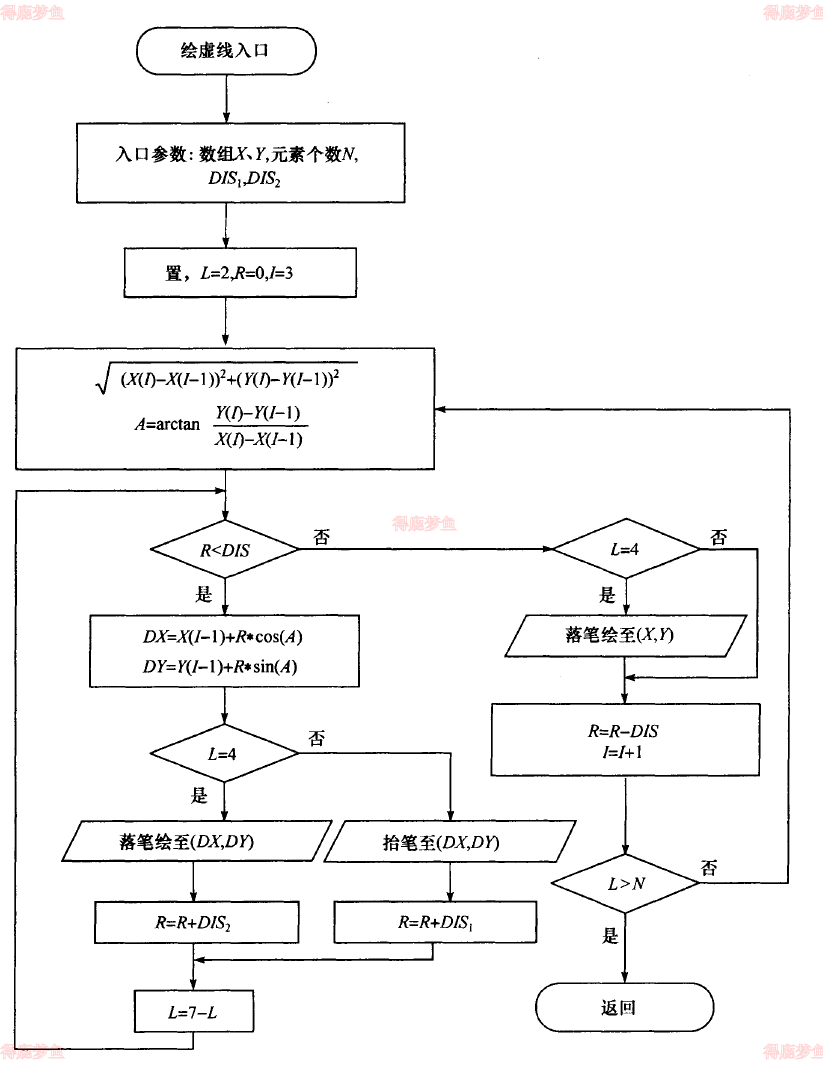
短齿线绘制
短齿线是由一条曲线和等间距垂直叠加在其上的许多短齿构成。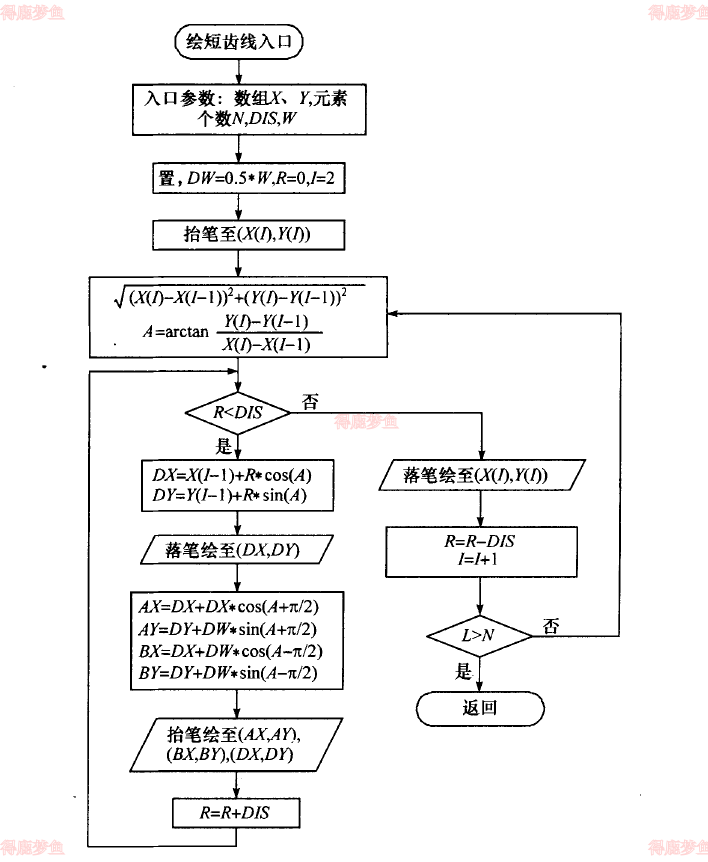
铁路线绘制
铁路线是地图上表示铁路分布状况和走向的符号。它是由一条双平行线和其中黑白相间的色块构成的。
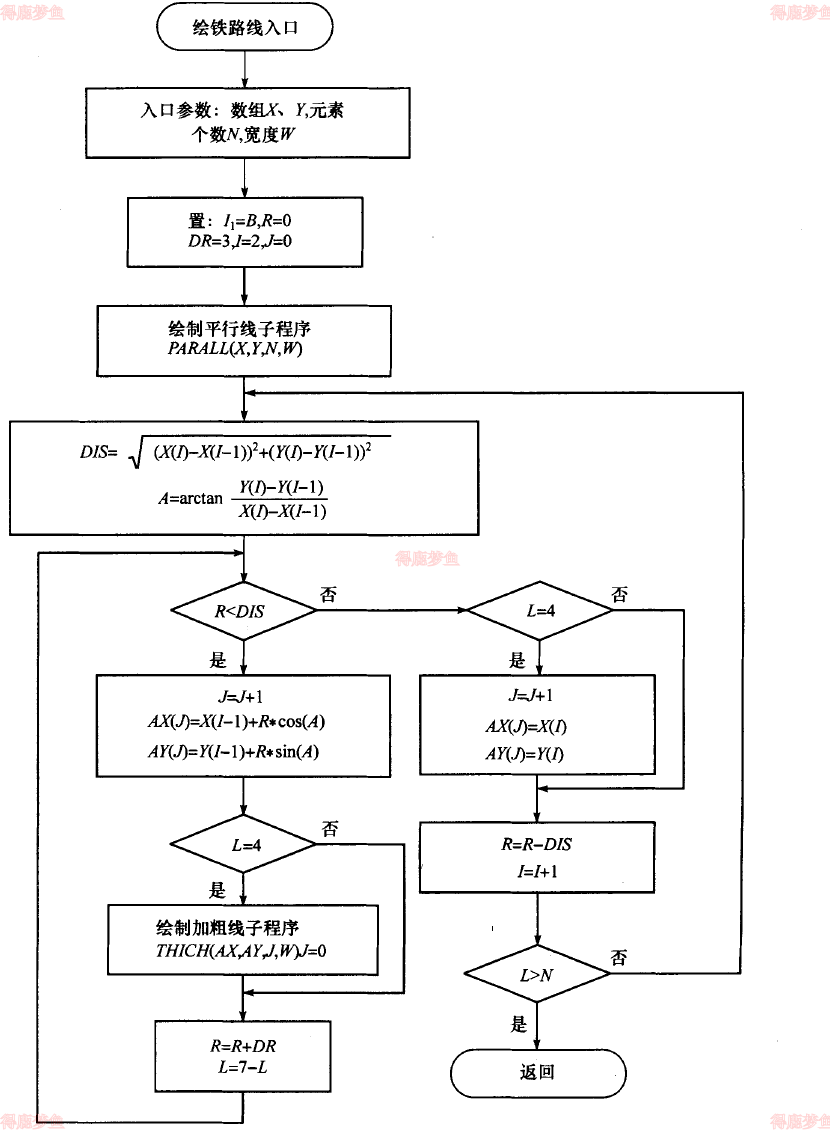
境界线的绘制
境界线是地图上表示国家或者行政区域边界轮廓以及范围的线状符号。使用较多。
国境界一般有相同大小的"I"型符号加点相同排列构成;省区界线一般有相同长度的虚线加点相间排列而成
设绘制境界线的参数为:定位曲线坐标xi,yi,i=1,2,3...;境界线中虚线的长度为DIS1,间距为DIS2,虚线2端齿线的宽度W,对一绘制省区境界线W=0;绘制方法如下:
首先将笔定位曲线端点x1,y1,若为>0, 则根据该点坐标、直线x1,y1−x2,y2的角度以及W求出,求出该点的齿线端点坐标,并绘出齿线,笔归起点x1,y1;若W=0,则不需要计算和绘制齿线。然后按定位曲线的方向和路径向前搜索并绘制到距离起点x1,y1曲线长度为DIS1的点x1′,y1′;若W>0,则根据该点坐标、所在直线的角度以及W求出过该点的齿缘端点坐标,绘出齿线。若W=0;则不需要计算和绘制齿线,在按照定位曲线的方向和路径向前搜索并求出距离点x1′,y1′曲线长度为DIS2的点x2′,y2′,在点2x1′+x2′,2y1′+y2′处绘点。将笔移至x2′,y2′作为起点。绘制下一个点,直至绘制完成境界线