矢量数据结构和栅格结构的相互转换,是地理信息系统的基本功能之一
矢量数据向栅格数据格式转化
矢量点的栅格化
根据下图,不难理解,将点的矢量坐标x,y转换为栅格行列号的公式为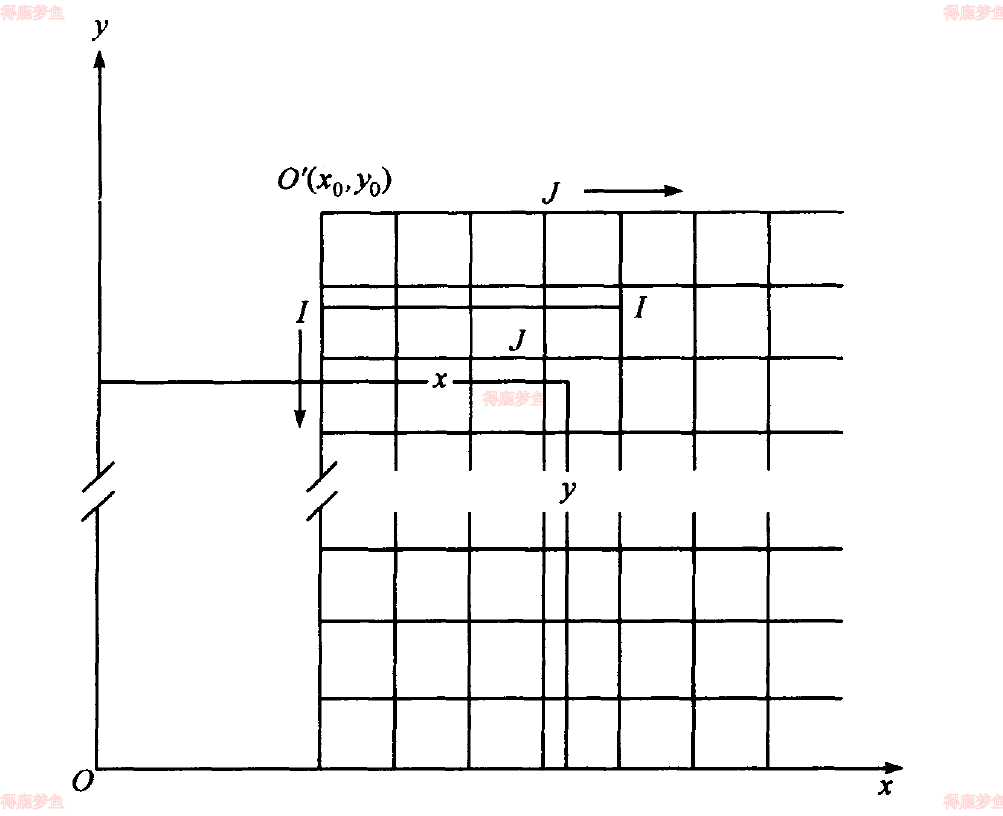
⎩⎨⎧I=1+[Dyy0−y]J=1+[Dxx−x0]
Dx是一个栅格的宽度
Dy是一个栅格的高度
[] 表示取整
矢量线的栅格化
在矢量数据中,曲线是由折线来逼近的
线栅格化的方法
- 八方向栅格化
根据矢量的倾角情况,在每行或者每列上,只有一个相元被涂黑(赋予不同于背景的灰度值),其特点是在保持八方向联通的前提下,栅格影像看起来是最细的,不同连线划间最不易“粘连”
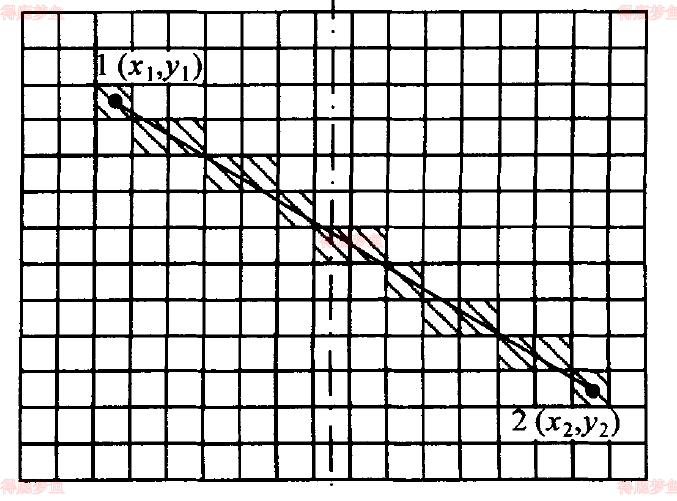
如下图所示,假定1和2为一条直线的2个端点,器坐标分别为x1,y1,x2,y2。首先按照1 确定行列号I1,J1,I2,J2,然后求出2个端点位置的行数差R和列数差L
如果 R > L 则逐行求出本行中心线与过这2个端点的直线的交点
⎩⎨⎧x=y−y1b+x1y=y中心线b=y2−y1x2−x1/assets/04
如果 R ≤ L 则逐列求出本列中心线与过这2个端点的直线的交点
⎩⎨⎧x=x中心线y=x−x1b+y1b=x2−x1y2−y1
- 全路径栅格化分带法
分带法: 即按行列计算起始列行号和终止列行号的方法
基于矢量的首末点以及倾角α的大小,可以计算出列号ie,ie或者列号je,je
当x2−x1 < y2−y1 计算行号ie,ie
当x2−x1 ≥ y2−y1 计算列号je,je
下面给列号x2−x1 ≥ y2−y1的计算方式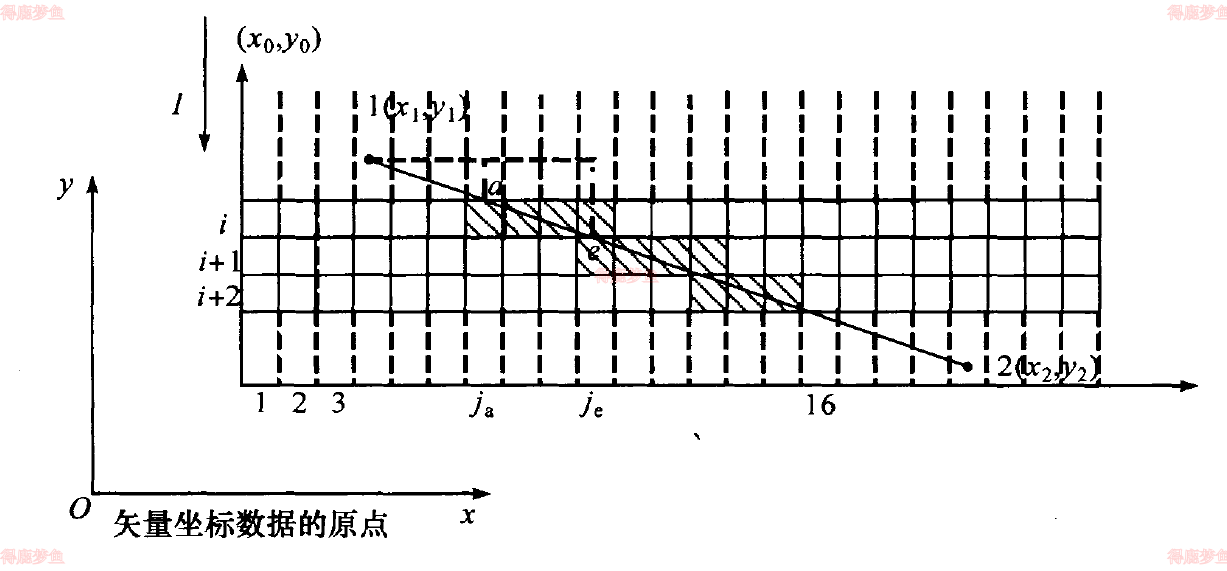
设当前处理行为第i行,栅格边长为m
计算倾角α的正切
tanα=x2−x1y2−y1计算起始列号ja
ja=[mtanαy0−i−1m−Y1+x1−x0]+1计算终止列号je
je=[mtanαy0−im−Y1+x1−x0]+1将第i行从第ja列开始到第je列为止的中间所有栅格涂黑
如果当前行不是终止行,则吧本行终止列号je为下行的起始列号ja;行号i+1转3处理 否则结束
矢量面的栅格化
矢量面格式向栅格面格式转也称为多边形填充。就是在矢量表示得四边形边界内部的所有栅格点上赋予想应得多边形编码
内部点扩散
该算法由每个多边形一个内部点种子点开始,并向其8个方向的=邻点扩散。判断各个新加入点是否在多边形的边界上,如果实在边界上,则该新加入的点不作为种子点,否则吧非边界点的邻点作为新的种子点与原有种子点一起进行新的扩散运算。并将该种子点赋予该多边形的编号。重复上述过程直到所有的种子点填满该多边形,并遇到边界停止为止。
射线算法和扫描算法
射线算法可逐点判断数据栅格点在某个多边形之外或者在多边形之内,有待判点向图外某点引射线。判断该射线与多边形所有边界相交的总次数。如果是偶数则判定为外部,否则为内部
扫描算法是射线算法的改进,将射线改为沿栅格阵列行或者列方向扫描线,判断与射线算法相似。
边界代数算法
边界代数多边形填充算法是一种积分思想的矢量格式向栅格格式转换算法。它适合于记录拓扑关系的多边形矢量数据转化为栅格结构。
基本思想: 对每幅地图的全部具有左右多边形编号的边界弧度,沿其前进的方向逐个搜索。当边界上行时,将边界线位置与左图框之间的网格点加上一个值=左多边形编号-右多边形编号;当边界线下行时,将边界线位置与左图框的栅格点加上一个值=右多边形编号-左多边形编号,而不管边界线的排列顺序。
栅格数据向矢量数据转换
栅格点坐标与矢量点坐标的关系
对于任意一个栅格点A而言,将其行、列号IJ转化为其中心点的x,y的公式如下
{x=X0+J−0.5Dxy=Y0+I−0.5Dy
栅格数据矢量化的基本步骤
- 边界提取:采用高通滤波将栅格图像二值化或以特殊值标识边界点
- 边界线追踪: 对每个边界弧段有一个结点向另一个结点搜索,通常对每个已知边界点沿除了进入方向的其他7个方向搜索下一个边界点,直到连成边界弧段
- 拓扑关系生成: 对于矢量表示的边界弧段数据,判断其与原图上各个多边形的空间关系,已形成完完整的拓扑结构并建立与属性数据的联系
- 去除多余点以及曲线圆滑;由于搜索是逐个栅格进行的,必须去除由此造成的多余点记录,以减少数据冗余;搜索结果,常用的算法有线形迭代法、分段三次多项式插入法、正轴抛物线平均加权法、斜轴抛物线平均加权法,样条函数插值法。
线状栅格数据的细化
线状栅格数据一般具有一定粗度且线划本身往往呈现粗细不匀的状态,线状栅格数据需要细化。已提取其中的轴线。这是因为
- 中轴线是栅格数据曲线的标准化存储形式。
- 实现细化是将栅格曲线矢量化的前提
- 在有些算法中可以提高计算精度
