得鹿梦鱼 得鹿梦鱼
知识库 前端技能树 面试题 学习资料 关于本人

几何变换_二维

应用于对象几何描述并改变它的位置、方向、或者大小的操作被称为几何变换
建模变换： 一般用于构造场景或者给出由多个部分组合而成的复杂对象的层次式描述等

基本的二维几何变换

平移、旋转和缩放是所有图形软件包中都含由的几何变换函数

平移

通过将位移量加到一个点的坐标上来生成一个新的坐标位置，可以实现一次平移
将平移距离tx,tyt_x, t_y加到原始坐标x,yx,y上获得一个新的坐标位置x′,y′x',y',可以实现一个二维位置的平移
{x′=x+txy′=y+ty\begin{cases}x' = x + t_x \\y' = y + t_y\end{cases}

tx,tyt_x, t_y被称为位移向量或者平移向量
平移是一种移动对象而不改变其形状的刚体变换。即对象上的每一个点都移动了同样的距离。

平移矩阵使用列向量表示为

[txty]\begin{bmatrix}t_x \\t_y\end{bmatrix}

旋转

通过指定一个旋转轴和一个旋转角度，可以进行一次旋转变换，在将对象的所有顶点按照指定角度绕指定旋转轴旋转后，该对象的所有点都可以旋转都新的位置

我们首先确定当基准点为坐标原点时位置P进行旋转的变换方程，如下图所示

点旋转

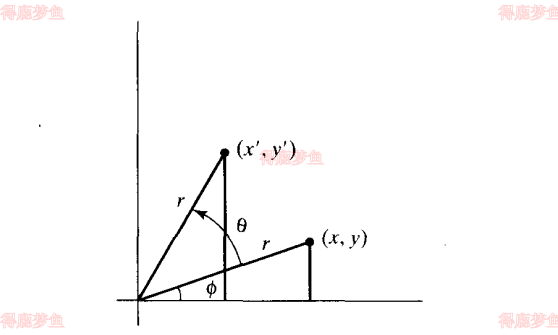
{x′=rcos⁡ϕ+θ=rcos⁡ϕcos⁡θ−rsin⁡ϕsin⁡θy′=rsin⁡ϕ+θ=rcos⁡ϕsin⁡θ+rsin⁡ϕcos⁡θ1\begin{cases}x' = r\cos \phi + \theta = r\cos \phi \cos \theta - r\sin\phi\sin\theta \\y' = r\sin \phi + \theta = r\cos \phi \sin \theta + r\sin\phi\cos\theta \\\end{cases}\tag{1}

{x=rcos⁡ϕy=rsin⁡ϕ2\begin{cases}x = r\cos\phi \\y = r\sin\phi\end{cases}\tag{2}
将2式带入1式中得到
{x′=xcos⁡θ−ysin⁡θy′=xsin⁡θ+ycos⁡θ1\begin{cases}x' =x\cos\theta - y\sin\theta \\y' =x\sin\theta + y\cos\theta\end{cases}\tag{1}

旋转矩阵使用矩阵形式表示为

[cos⁡θ−sin⁡θsin⁡θcos⁡θ]\begin{bmatrix}\cos\theta & -\sin\theta \\\sin\theta & \cos\theta\end{bmatrix}

旋转是一种移动对象而不改变其形状的刚体变换

缩放

改变一个对象大小，可使用缩放变换，一个简单的二维操作可以通过将缩放系数sx,sys_x, s_y与对象坐标位置相乘得到

{x′=x⋅sxy′=y⋅sy\begin{cases}x' = x \cdot s_x\\y' = y \cdot s_y\end{cases}

缩放矩阵使用矩阵形式表示为

[sx00sy]\begin{bmatrix}s_x & 0 \\0 & s_y\end{bmatrix}

可以赋值给缩放系数sx,sys_x, s_y任何正数值，值小于1表示缩小，大于表示放大，如果sx,sys_x, s_y是相同的则产生一致缩放，否则是差值缩放

矩阵表示和齐次坐标

齐次坐标

如果将2×22 \times 2的矩阵扩充为3×33 \times 3矩阵，就可以吧二维几何变换的乘法和平移项组合称为单一矩阵表示，
标准的实现技术是将二维坐标位置表示x,yx,y扩充表示为三维坐标xh,yh,hx_h,y_h,h,称为齐次坐标，这里的齐次参数h是一个非零值

平移矩阵齐次坐标表示

[x′y′1]=[10tx01ty001]⋅[xy1]\begin{bmatrix}x' \\y' \\1\end{bmatrix}\text{=}\begin{bmatrix}1 & 0 & t_x\\0 & 1 & t_y\\0 & 0 & 1\end{bmatrix}\cdot\begin{bmatrix}x \\y \\1\end{bmatrix}

旋转矩阵齐次坐标表示

[x′y′1]=[cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001]⋅[xy1]\begin{bmatrix}x' \\y' \\1\end{bmatrix}\text{=}\begin{bmatrix}\cos\theta & -\sin\theta & 0\\\sin\theta & \cos\theta & 0\\0 & 0 & 1\end{bmatrix}\cdot\begin{bmatrix}x \\y \\1\end{bmatrix}

缩放矩阵齐次坐标表示

[x′y′1]=[sx101sy0001]⋅[xy1]\begin{bmatrix}x' \\y' \\1\end{bmatrix}\text{=}\begin{bmatrix}s_x & 1 & 0\\1 & s_y & 0\\0 & 0 & 1\end{bmatrix}\cdot\begin{bmatrix}x \\y \\1\end{bmatrix}

逆变换

对于平移，我们通过对平移距离取负值而得到逆变换矩阵
对于旋转，我们通过将旋转角度取负值而得到逆变换矩阵
对于缩放，我们通过将缩放系数取倒数而得到逆变换矩阵

复合变换

利用矩阵表达式，我们可以通过计算单个变换的矩阵乘积，将任意序列组合复合变换矩阵，形成变换矩阵的乘积经常被称为矩阵的合并或复合

通用二维基准点旋转

  1. 平移对象使基准点位置移动到坐标原点
  2. 绕坐标原点旋转
  3. 平移对象使基准点回到其原始位置

通用二维基准点缩放

  1. 平移对象使基准点位置移动到坐标原点
  2. 绕坐标原点缩放
  3. 平移对象使基准点回到其原始位置

其他二维变换

反射

产生对象镜像的变换被称为反射，

关于y轴的反射
[1000−10001]\begin{bmatrix}1 & 0 & 0\\0 & -1 & 0\\0 & 0 & 1\end{bmatrix}

关于x轴的反射
[−100010001]\begin{bmatrix}-1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix}

关于坐标原点的反射
[−1000−10001]\begin{bmatrix}-1 & 0 & 0\\0 & -1 & 0\\0 & 0 & 1\end{bmatrix}

关于y=x的反射
[010100001]\begin{bmatrix}0 & 1 & 0\\1 & 0 & 0\\0 & 0 & 1\end{bmatrix}

关于y=-x的反射
[0−10−100001]\begin{bmatrix}0 & -1 & 0\\-1 & 0 & 0\\0 & 0 & 1\end{bmatrix}

错切

是一种时对象形状发生变化的变换，经过错切的对象好像是由已经相互滑动的内部夹层组成，

移动x坐标的错切
[1shx−shx⋅yref110001]\begin{bmatrix}1 & sh_x & -sh_x \cdot y_ref\\1 & 1 & 0\\0 & 0 & 1\end{bmatrix}
移动y坐标的错切
[100shy1−shy⋅xref001]\begin{bmatrix}1 & 0 & 0\\sh_y & 1 & -sh_y \cdot x_ref \\0 & 0 & 1\end{bmatrix}

二维坐标系之间的变换

到目前为止，我们讨论了对于点的变换，所有这些点都是相对于一个特定的坐标系来表示的。这个坐标系称为世界坐标系。
我们有一些物体，而每一个物体都有物体自身的坐标系的一组顶点来定义，这种坐标被称为局部坐标系。

将一个带有局部坐标系的物体放到世界坐标系中的一个位置的变换称为模型变换

从世界坐标系向局部坐标系的变换称为观察变换

  1. 将x'y'系统的坐标原点x_0,y_0平移到xy系统的坐标原点
  2. 将x'轴旋转到x轴

T−x0,−y0=[10−x001−y0001]T -x_0, -y_0 =\begin{bmatrix}1 & 0 & -x_0\\0 & 1 & -y_0\\0 & 0 & 1\end{bmatrix}

Rθ=[cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001]R\theta=\begin{bmatrix}\cos\theta & -\sin\theta & 0\\\sin\theta & \cos\theta & 0\\0 & 0 & 1\end{bmatrix}

复合矩阵表示Mx′y′,xy=T−x0,−y0Rθ\bold M_{x'y',xy} = T -x_0, -y_0R\theta

几何变换_二维
≡