填充区图元

除了点、线之外，还有一种描述图形组成部分的有用结构就是使用某种颜色或者图案进行填充的区域。这种类型的图形部分一般被称为填充区或者填充的区域。

使用一组多边形面片描述的对象被称为标准图形对象或者图形对象

多边形填充区

一个多边形在数学上的定义是：由是三个或者更多的顶点坐标位置描述的平面图形，这些顶点由成称为多边形的边顺序连接

多边形分类

多边形的一个内角是由两条相邻边形成的多边形边角之内的角。如果一个多变形的所有内角均小于 $180^\circ$ ，则该多边形被成为凸多边形。
不是凸多边形的多边形被称为凹多边形
退化多边形常用来描述共线或者重叠坐标位置的顶点集。为了软件的鲁棒性，图形软件包可以拒绝退化或者非平面坐标集。

识别凹多边形

凹多边形至少有一个内角是大于 $180^\circ$ 的,凹多边形某些边的延长线会与其他边相交有时一对内点连线会与多边形边界相交

方法一：如果为每一个边建立一个向量，则可以使用相邻边的叉积来测试凹凸性，凸多边形的所有向量叉积均同号。因此如果某些叉积取正值而另一些取负值，则可确定其为凹多边形
请参考叉积

方法二：观察多边形顶点位置与每条边延长线的关系，如果有些顶点在某些延长线的一侧而其他的一些顶点在另一侧，则多边形为凹多边形
请参考延长线算法

内-外测试

奇偶规则和非零环绕规则是识别平面图形内部区域的两种常用方法

奇偶规则

从任意位置P到对象坐标范围以外的远点画一条概念上的射线，并统计改射线与各边的交点数目，如果相交的的边数是奇数，则是内部点，否则是外部点，为了得到精确的相交边数，必须确认所画的直线不与任何多边形的顶点相交

代码实现: 请参考点与平面图形的位置关系-奇偶原则算法

非零环绕规则

统计多边形边以逆时针方向环绕某个特定点的次数，这个被称为环绕数

将二维对象的内部点定义为具有非零值的环绕数，在对多边形应用非零环绕数规则时，将环绕数初始化为零，设想从任意位置p到对象坐标范围外的的一点画一条射线，所选择的射线不与多边形的任何顶点相交，当从点p沿射线方向移动时，统计穿过改该射线的边的方向，每当多边形从右到左穿过射线时，边数加一，否则减一，当穿过所有的边后，环绕数决定了P的相对位置，环绕数非零，则为内部点，否则外部点

代码自行实现: 部分代码可参考点与平面图形的位置关系-奇偶原则算法

和奇偶规则相比由于加入了方向性的判断，所以在由孔洞的复杂多边形的判断会与奇偶规则的判断结果有所不同

剖分多边形

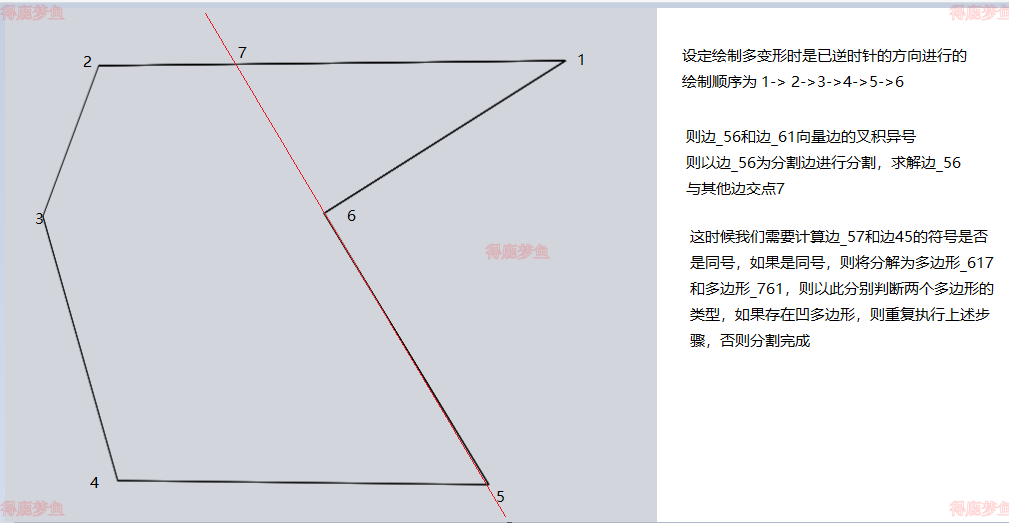
一旦识别出凹多边形，我们就需要将其切割成为多个凸多边形

对于多边形的任意顶点s来说，多边形中所有顶点与s连续形成的线段，若全部在多边形的内部或者边上面，则成为s为可视点

寻找到一个凹点
寻找和凹点相连的可视点信息
选择其中的某一个可视点将其拆分为两个子多边形，
递归判断子多边形是不是凹多边形如果是递归上述如果不是结束

剖分凹多边形

代码实现: 请参考剖分多边形