改进的加权剖分简单多边形为凸多边形的算法

请优先阅读一个加权剖分简单多边形为凸多边形的算法
本文的内容来自于燕山大学学报第25卷第1期的内容

简单多边形剖分是计算几何中的一类基本问题，剖分算法在图像处理、模式识别、CAD/CAM以及计算机图形学等领域应用较广

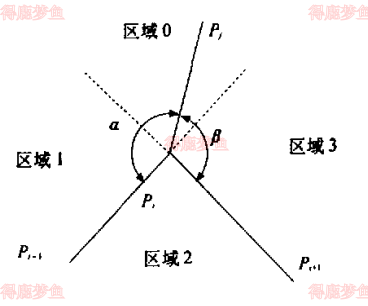
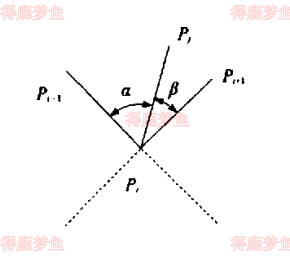
设$p_j$是从点$p_i$发出的剖分线的另个端点，$\vec{p_ip_j}$和$\vec{ p_ip_{i-1}}$的夹角为$\alpha$，$\vec{p_ip_j}$和$\vec{ p_ip_{i+1}}$的夹角为$\beta$

从下图中不难看出，角$\alpha$和$\beta$的差值$\alpha - \beta$可以描述从$p_i$发出的剖分线所在的区域,当剖分线位于区域0的角平分线上时，$\alpha - \beta=0$, 当剖分线想两侧靠拢时，$\alpha - \beta$逐渐增大，当点落在构成区域2的两条边上时，$\alpha - \beta$取最大值

凹点	凸点

由于$\alpha, \beta$在0和$\pi$上取值，而余弦函数在此区间内是单调的，因此可是使用余弦函数代替$cos\alpha - cos \beta$
设向量$u_1$是边向量$\vec{p_{i-1}p_i}$的单位向量，向量$u_2$是边向量$\vec{p_{i}p_{j+1}}$的单位向量，向量$u_3$是边向量$\vec{p_{i}p_j}$的单位向量，
则更具向量内积有
$cos \alpha = u_1 \cdot u_3 = x_1x_3 + y_1y_3$
$cos \beta = u_2 \cdot u_3 = x_2x_3 + y_2y_3$