一种凹多边形凸分解的全局剖分算法

请优先阅读改进的加权剖分简单多边形为凸多边形的算法
请优先阅读一个加权剖分简单多边形为凸多边形的算法
本文的内容来自于中国民航大学学报第29卷第3期的内容

基本概念和定义

简单多边形： 设平面上有n个点$p_1, p_2, ... , p_n$按循环顺序方法逆时针排列,$p_1$在$p_n$后，又设$\vec e_0 = \vec{p_0p_1} , \vec e_1 = \vec{p_1p_2} , ... , \vec e_1 = \vec{p_np_0}$是连接点的n条线段，那么这些线段界限形成一个简单多边形

若多边形P的顶点序列$p_0, p_1, ..., p_n$按照逆时针方向排列，并且点$p_{i+1}$在$p_{i-1}p_i$的左右侧，则点为凸凹点

对于多边形的任意顶点s来说，多边形中所有顶点与s连续形成的线段，若全部在多边形的内部或者边上面，则成为s为可视点。

如下图所示，点$s_4$不是可视点，应为$s_4$同顶点$s_1,s_7，s_{12}$的连线不完全在多边形轮廓内

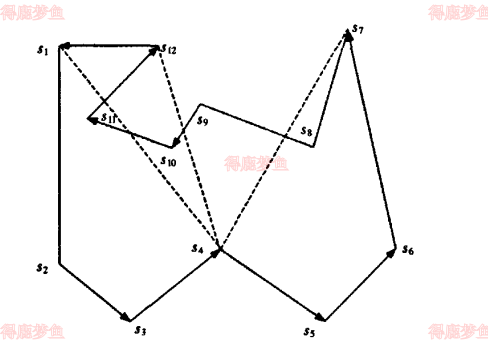
最佳剖分： 如果剖分线连接2个凹点，同时这2个凹点在分属的两个子多边形上表现为凸点，即为最佳剖分

正负法： 对于任意直线方程$Fx,y=0$可以吧平面分为3个区域分别为
$$\begin{cases}Fx,y = 0 \text{在线上} \\Fx,y > 0 \text{F+区,线右侧} \\Fx,y < 0 \text{F-区,线左侧}\end{cases}$$

局部剖分算法

是指每次剖分只针对一个凹点，并只考虑如何引出剖分线来消除当前凹点的算法

原理

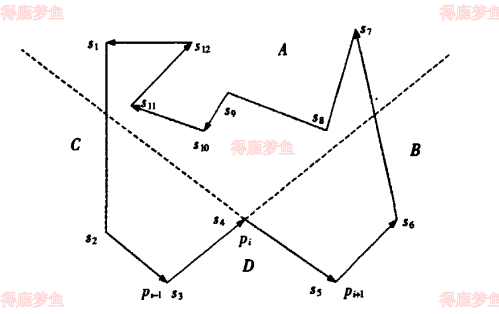
如下图所示，从多边形的第一个顶点$s_1$开始搜索，搜索到第一个凹点记录为$p_i$, 记录沿着轮廓线防线之前和之后相邻的点，并标记为$p_{i-1}、p_{i+1}$,沿着$p_{i-1}p_i$、$p_{i+1}p_{i}$方向把轮廓线分为A、B、C、D四个区域，其中
A：射线$p_{i-1}p_i$和$p_{i+1}p_{i}$形成的扇形区域
B：射线$p_{i-1}p_i$和$p_{i+1}p_{i}$形成的反向扇形区域
C：射线$p_{i+1}p_i$和$p_{i-1}p_{i}$形成的扇形区域
D：射线$p_{i+1}p_i$和$p_{i-1}p_{i}$形成的反向扇形区域

存在的问题

1. 一次剖分消去两个凹点形成最佳剖分的概率比较小
2. 无法保证剖分后的多边形形态质量

全局剖分算法

首先对当前轮廓上的所有凹点进行最佳剖分点的处理，然后从其中选取当前轮廓的最优剖分点进行剖分

可视点串求解算法

正负法原理来搜索可视点串，更正其在求取B区内最后一点和C区内第一个点时可能出现的错误，改进如何确定可视点串的算法，如上图所示
记$p_{i-1}pi$方向的直线方程为$F_{i-1}x,y$,记$p_{i+1}p_i$方向的直线方程为$F_{i+1}x,y$,则在A区域内的点应该满足的条件是$F_{i-1}x,y \leq 0$并且$F_{i+1}x,y \geq 0$,由于可视点串是在A区域内的点，但是轮廓线上出现在A区域的顶点不一定都是可视点，因此首先得到A区域的顶点之后再筛选可视点

区域A可视点串的求取

首先通过一遍搜索确定轮廓线P在A区域内的顶点并将其添加凹临时点串tempA中，$p_i$指向当前凹点的顶点指针，从凹点$p_i$的后继节点p沿着逆时针方向开始搜索，知道重搜索到凹点$p_i$为止
当得到凹点$p_i$位于A区的轮廓点串后，根据可视点的定义得到可视点串SA，

最佳剖分点的选取

对于权函数的选取，主要的算法思想是：尽量是的剖分线在凹点的角平分线上，这样可以保证使得凹点剖分后的两个角相差不大，保证剖分后的形态质量

算法描述

1. 遍历简单多边形P，建立凹点库，以此从P中取出顶点，判断是否是凹点，如果是凹点，记录其前驱和后继并标识为未访问，添加到凹点库中
2. 以此搜索凹点穿中未访问的凹点，采用改进的求解算法求出可视点串SA以及B区内最后一点和C区内第一点
3. 遍历凹点穿，利用权函数从每个凹点中找到最优的剖分点、权值和剖分类型并保存。
4. 遍历凹点串根据剖分类型的权值找出最佳剖分点（剖分类型1凹点->2凸点->3辅助点）
5. 根据凹点和剖分点分解原多边形形成两个新的多边形并添加到多边形链表中，同时从多边形链表中删除原多边形，递归上述过程知道没有凹点为止