椭圆的生成算法_中点椭圆算法

考虑标准位置的椭圆在四分象限中是对称的，因此我们必须计算一个象限中椭圆曲线的像素位置，在由对称性得到其他象限的像素位置，如下图

中点椭圆算法

首选确定以原点为中心的标准位置椭圆上的点$x,y$,然后将这些点平移到以$x_c,y_c$为中心的椭圆上

中点椭圆算法将分为两部分应用与第一象限，划分的一句是斜率的具体对小于 1 在 x 轴取单位不长，在斜率绝对值大于 1 的区域在 y 轴取单位步长来处理第一象限内的像素点位，如下图所示

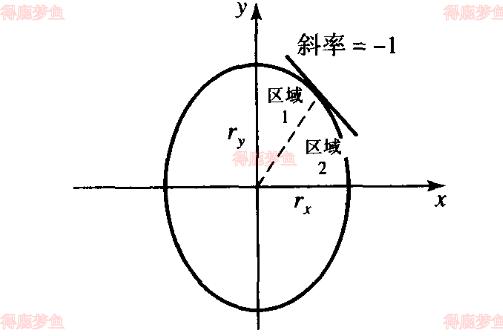
可以从位置$0, r_y$开始，在第一象限内沿着椭圆路径顺时针绘制，当斜率便于-1 时，将 x 方向的单位步长转为 y 方向的单位步长。
利用并行处理器，则可以同时计算两个区域内的像素位置

取椭圆的中心点为$0,0$, 则椭圆的定义函数表示为
$\frac{x - x_c}{r_x}^2 + \frac{y - y_c}{r_y}^2 = 1$
$$f_{ellipse} = r_y^2x^2 + r_x^2y^2 - r_x^2r_y^2 \tag{1}$$

决策函数为：

$$\begin {cases}f_{ellipse} < 0 \text{在椭圆边界内} \\f_{ellipse} = 0 \text{在椭圆边界上} \\f_{ellipse} > 0 \text{在椭圆边界外}\end {cases}$$

从$0,r_y$开始，在 x 方向取单位步长到区域的分界处，也就是斜率为-1 的点，然后转为 y 方向的单位步长，覆盖完第一象限内的所有点位，在每一步中，需要检测曲线的斜率值，

有 1 式可以计算斜率为
$$\frac{dy}{dx} = -\frac{2r_y^2x}{2r_x^2y}$$
在区域交界处有$dy/dx = -1$则$2r_y^2x = 2r_x^2y$
因此在区域1存在$2r_y^2x < 2r_x^2y$
在区域2存在$2r_y^2x >= 2r_x^2y$
如同圆一样，假设刚在$x_k,y_k$上绘制了一个像素，下一个像素的位置则为$x_k + 1,y_k$或者$x_k+ 1,y_k - 1$, 看那个更接近圆，也就是距离$x_k+1, y_k - \frac{1}{2}$那个更近

$p1_k = r_y^2x_k + 1^2 + r_x^2y_k - \frac{1}{2}^2 - r_x^2r_y^2$

在区域1内下一个取样位置为$x_{k+1} = x_k + 2$
$p1_k < 0, \text{时} p1_{k+1} = r_y^2x_k + 2^2 + r_x^2y_{k+1} - \frac{1}{2}^2 - r_x^2r_y^2$
$p1_k >= 0, \text{时} p1_{k+1} = r_y^2x_k + 2^2 + r_x^2y_{k+1} - \frac{1}{2}^2 - r_x^2r_y^2$

$$\begin {cases}p1_k < 0 \text{时} p1_{k+1} - p1_k = 2r_y^2x_{k+1} + r_y^2 \\p1_k >= 0 \text{时} p1_{k+1} - p1_k = 2r_y^2x_{k+1} + r_y^2 - 2r_x^2y_{k+1}\end {cases}$$

在区域2内

$p2_k = r_y^2x_k + \frac{1}{2}^2 + r_x^2y_k - 1^2 - r_x^2r_y^2$
在区域2内下一个取样位置为$y_{k+1} = y_k - 2$

$p2_k < 0, \text{时} p2_{k+1} = r_y^2x_{k+1} + \frac{1}{2}^2 + r_x^2y_{k} - 1^2 - r_x^2r_y^2$
$p2_k >= 0, \text{时} p2_{k+1} = r_y^2x_{k+1} + \frac{1}{2}^2 + r_x^2y_{k} - 2^2 - r_x^2r_y^2$

生成算法如下

1. 输入$r_x, r_y$,得到椭圆的第一个点$0, r_y$
2. 计算区域1的决策制的初始值$p1_0 = r_y^2 -r_x^2r_y + \frac{1}{4}r_x^2$
3. 在区域1中的每个x_k位置，从k=0,完成下述
   如果$p1_k < 0$,下一个点为$x_k + 1, y_k, p1_{k+1} = p1_k + 2r_y^2x_{k+1} +r_y^2$
   否则 下一个点为$x_k + 1, y_k - 1, p1_{k+1} = p1_k + 2r_y^2x_{k+1} +r_y^2 - 2r_x^2y_{k+1}$
   直到$2r_y^2x >= 2r_x^2y$
4. 使用区域1中计算出的最后一个点$x_1,y_1$为开始点来计算区域2的初始值$p2_0 = r_y^2x_1 + \frac{1}{2}^2 + r^2_xy_1 - 1^2 - r_x^2r^2_y$
5. 在区域1中的每个y_k位置，从k=0,完成下述
   如果$p2_k < 0$,下一个点为$x_k, y_k - 1, p2_{k+1} = p2_k - 2r_x^2y_{k+1} +r_x^2$
   否则 下一个点为$x_k + 1, y_k - 1, p2_{k+1} = p2_k + 2r_y^2x_{k+1} +r_x^2 - 2r_x^2y_{k+1}$
   直到$y=0$

请参考中点画椭圆算法