梁友栋-barsky线段裁剪算法
它基于分析线段的参数化方程
对端点为x0,y0,x1,y1的直线段,可使用参数形式描述为
{x=x0+ux1−x0y=y0+uy1−y0
与点裁剪的条件结合则有
{xwmin≤x0+ux1−x0≤xwmaxywmin≤y0+uy1−y0≤ywmax
展开上式,表示为upk≤qk1
⎩⎨⎧xwmin≤x0+ux1−x0⇒xwmin−x0≤uΔx⇒u−Δx≤x0−xwminx0+ux1−x0≤xwmax⇒uΔx≤xwmax−x0⇒uΔx≤xwmax−x0ywmin≤y0+uy1−y0⇒ywmin−y0≤uΔy⇒u−Δy≤y0−ywminy0+uy1−y0≤ywmax⇒uΔy≤ywmax−y0⇒uΔy≤ywmax−y0
pk=0
线段平行于裁剪窗口的边界中的任意一条
满足qk<0
则线段完全在裁剪窗口外如下图所示
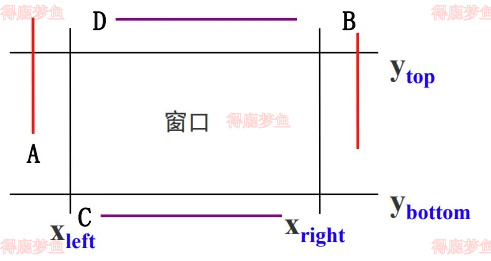
如果qk≥0
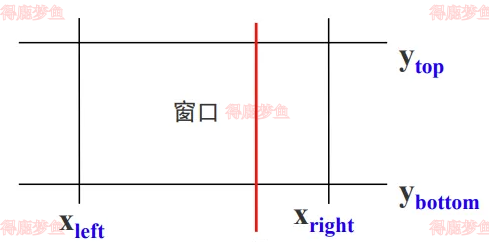
pk=0
当pk<0线段从裁剪边延长线的外部延伸到内部,是入边交点
当pk>0线段从裁剪边延长线的内部延伸到外部,是出边交点
线段和窗口一共有4个交点,根据pk的符号,就可以知道那个入点,那个是出点,如下图中的ul,ur,ut,ub,在加上两个端点的u=0,1,一共6个u值
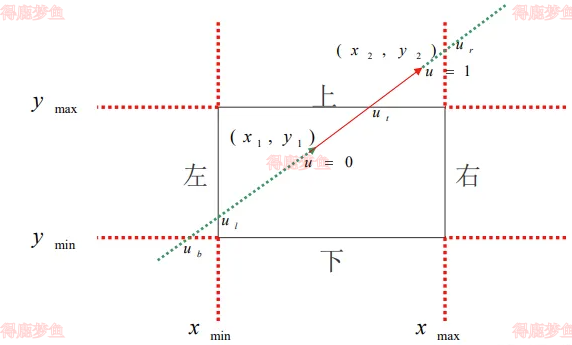
根据1式的得出
u=pkqk
6个u值分别为
⎩⎨⎧us=0ue=1ul=−Δxx0−xwminur=Δxxwmax−x0ut=Δyywmax−y0ub=−Δyy0−ywmin
把pk<0的两个u值和0比较去找大的
当Δx>0 && Δy>0 取ul,ub
当Δx>0 && Δy<0 取ul,ut
当Δx<0 && Δy>0 取ur,ub
当Δx<0 && Δy<0 取ur,ut
把pk>0的两个u值和1比较去找小的
当Δx>0 && Δy>0 取ur,ut
当Δx>0 && Δy<0 取ur,ub
当Δx<0 && Δy>0 取ul,ut
当Δx<0 && Δy<0 取ul,ub
| 条件 | pk<0[umax] | pk>0[u_{min}] |
|---|
| Δx>0 && Δy>0 | maxul,ub,0 | minur,ut,1 |
| Δx>0 && Δy<0 | maxul,ut,0 | minur,ub,1 |
| Δx<0 && Δy>0 | maxur,ub,0 | minul,ut,1 |
| Δx<0 && Δy<0 | maxur,ut,0 | minul,ub,1 |
如果umax>umin 则直线段在窗口外面删除
如果umax≤umin 求出交点坐标
注意u的有效范围是[0,1]
请参考梁友栋-barsky线段裁剪算法



