一个加权剖分简单多边形为凸多边形的算法

本文的内容来自于计算机学报第21卷第3期的内容

权函数

剖分简单多边形为凸多边形要通过逐次加入剖分线来消除凹点，如果加入的一条剖分线连接了两个凹点，两个凹点转化为分属的两个子多边形，在每个子多边形中都表现为凸点，这是所做的剖分是最佳剖分，理想的情形是每次都做最佳剖分，记每次都能唯一的找到一条可构成最佳剖分的剖分线，逐次就爱如这样的剖分线就完成了剖分，但实际上最佳剖分有时会不存在，有时又会有多个
如果简单多边形中两个顶点间的连线全部都落在多边形内部，则这两个顶点式彼此可视的，容易理解剖分问题实际上就是挑选一些彼此可视的顶点对，并连接作为加入的剖分线，可见只要能够建立一种适当的权函数，就能够每次都按照权值最大而唯一确定的挑选出应加入的剖分线

为建立适当的权函数需要考察他具有的性质，设点$p_i$是简单多边形中一个待消除的凹点，过点$p_i$的前后两条边做直线，将平面划分为四个区域如下图

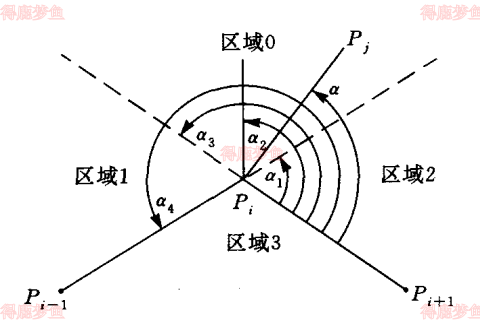
要想在点$p_i$处得到最佳剖分，从点$p_i$处发出的剖分线必须落在区域0中,如果落在区域1或者区域3中，那么其分属的2个子多边形中表现为一个是凸点一个是凹点，区域2是剖分线不能落入的多边形外部

从简单多边形任意个一点顶点$p_i$发出剖分线可以取得权值为

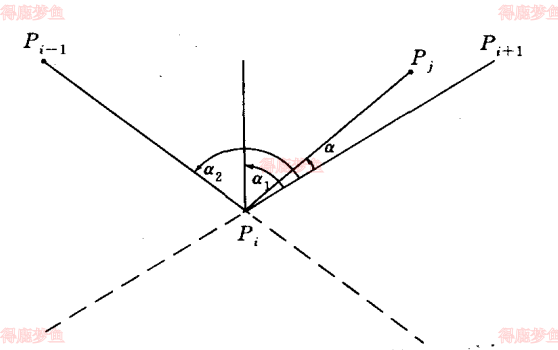
$$\begin{cases}\omega p_i = f\alpha \text{若点是凹点,三个点形成右转} \\\omega p_i = f\alpha \text{若点是凸点,三个点形成左转}\end{cases}$$

其中$m a x_1$和$m a x_2$是事先给定的控制参数，分别对应了两种情形的极大值

$$\begin{cases}fa = m a x_1 \frac{\alpha}{\alpha_1} 0 < \alpha < \alpha_1 \\fa = m a x_1 1 + \frac{\alpha - \alpha_1}{\alpha_2 - \alpha_1} \alpha_1 \leq \alpha < \alpha_2 \\fa = m a x_1 2 - \frac{\alpha - \alpha_2}{\alpha_3 - \alpha_2} \alpha_2 \leq \alpha < \alpha_3 \\fa = m a x_1 1 - \frac{\alpha - \alpha_3}{\alpha_4 - \alpha_3} \alpha_3 \leq \alpha < \alpha_4 \\fa = 0 \text{其他}\end{cases}$$

$$\begin{cases}ga = m a x_2 \frac{\alpha}{\alpha_1} 0 < \alpha < \alpha_1 \\ga = m a x_1 1 + \frac{\alpha - \alpha_1}{\alpha_2 - \alpha_1} \alpha_1 \leq \alpha < \alpha_2 \\ga = 0 \text{其他}\end{cases}$$

算法描述

1. 检查并标记简单多边形的凹顶点
2. 确定简单多边形中至少有一个凹点的所有可视点对
3. 为每组可视点计算权值
4. 对已得到的所有可视点进行按权值排序
5. 逐次加入剖分线实现剖分