圆的生成算法_中点画圆算法

考虑圆的对称性，可以有效的减少计算量，圆的形状在 每个象限中是相似的，因此瑞如果我们确定了再第一象限中圆的位置 ，就可以生成圆在xy平面中其他象限的部分，如下图

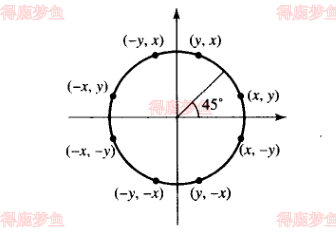
我们仅需要计算的是从$x =0$到$x =y$分段内的点就可以得到整个圆的所有像素位置
使用圆的参数方程和极坐标方式求解，仍然需要大量的计算时间，根据有效的画圆算法是如同bresenham画线算法一样以决策函数的增量计算为基础

为简单期间设原点坐标为坐标轴的中心点坐标
考虑绘制圆的方向为顺时针方向
如同光栅画线算法，我们在每个步中以单位间隔取样并确定离指定圆最近的像素位置，对于给定半径r，圆弧度为从x=0到x=y,曲线的斜率从0变化为-1，因此可以在该八分圆的正x方向去单位步长，使用决策函数来决定每一步中的两个可能得y值，那个更接近圆的位置
$$\begin {cases}f_{circ} = x^2 + y^2 - r^2 < 0 \text{在圆边界内} \\f_{circ} = x^2 + y^2 - r^2 = 0 \text{在圆边界上} \\f_{circ} = x^2 + y^2 - r^2 > 0 \text{在圆边界外}\end {cases}$$

假设刚在$x_k,y_k$上绘制了一个像素，下一个像素的位置则为$x_k + 1,y_k$或者$x_k+ 1,y_k - 1$, 看那个更接近圆， 也就是距离$x_k+1, y_k - \frac{1}{2}$那个更近
$p_k = f_{circ}x_k+1, y_k - \frac{1}{2} = x_k+1^2 + y_k - \frac{1}{2}^2 - r^2$
设定$p_k< 0$, 中点在圆内，$y_k$接近圆边界，否则$y_k - 1$接近圆边界

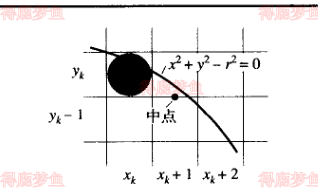
$p_{k+1} = x_{k+1}+1^2 + y_{k+1} - \frac{1}{2}^2 - r^2$
$p_{k+1} = x_k+2^2 + y_{k+1} - \frac{1}{2}^2 - r^2$
$p_{k+1} = x_k^2 + 2x_k + 4 + y_{k+1} - \frac{1}{2}^2 - r^2$

$p_{k+1} - p_k = x_k^2 + 4x_k + 4 + y_{k+1} - \frac{1}{2}^2 - r^2 - x_k+1^2 + y_k - \frac{1}{2}^2 - r^2$
$p_{k+1} - p_k = x_k^2 + 4x_k + 4 + y_{k+1} - \frac{1}{2}^2 - r^2 - x_k^2 + 2x_k + 1 + y_k - \frac{1}{2}^2 - r^2$
$p_{k+1} - p_k = x_k^2 + 4x_k + 4 + y_{k+1} - \frac{1}{2}^2 - r^2 - x_k^2 - 2x_k - 1 - y_k - \frac{1}{2}^2 + r^2$
$p_{k+1} - p_k = 3 + 2x_k + y_{k+1} - \frac{1}{2}^2 - y_k - \frac{1}{2}^2$
$p_{k+1} - p_k = 3 + 2x_k + y_{k+1}^2 - y_{k+1} + \frac{1}{4} - y_k^2 - y_k + \frac{1}{4}$
$p_{k+1} - p_k = 3 + 2x_k + y_{k+1}^2 - y_{k+1} + \frac{1}{4} - y_k^2 + y_k - \frac{1}{4}$
$p_{k+1} - p_k = 3 + 2x_k + y_{k+1}^2 - y_{k+1} - y_k^2 + y_k$
$p_{k+1} - p_k = 3 + 2x_k + y_{k+1}^2 - y_k^2 - y_{k+1} - y_k$
$p_{k+1} = p_k + 3 + 2x_k + y_{k+1}^2 - y_k^2 - y_{k+1} - y_k$
$p_{k+1} = p_k + 1 + 2x_k + 1 + y_{k+1}^2 - y_k^2 - y_{k+1} - y_k$
其中$y_{k+1}$是$y_k$还是$y_k - 1$取决去$p_k的符号$

生成算法如下：

1. 求初始误差, 将$0, r$坐标带入$p_0 = 1 + r - \frac{1}{2}^2 - r^2 = \frac{5}{4} - r$
2. 求下一个光栅点$x_{k+1} = x_k + 1$
   如果$p_k < 0$, 则$y_{k+1} = y_k$
   否则选择为$y_{k+1} = y_k - 1$
3. 绘制$x_{k+1}, y_{k+1}$,
4. 计算差值$P_{k+1} = P_k + 1 + 2x_k + 1 + y_{k+1}^2 - y_k^2 - y_{k+1} - y_k$,
   若$p_k<0$ 则$P_{k+1} = p_i + 3 + 2x_k$
   否则$P_{k+1} = p_i + 1 + 2x_k - y_k$
5. 如果x >= y 则终止循环否则执行2,3,4

代码实现

请参考中点画圆算法