Nicholl-lee-Nicholl线段裁剪算法

是在裁剪窗口创建多个区域，从而避免对一个直线段进行多次裁剪，

确定一条直线完全在裁剪窗口内部或者外部的初始测试可以想前面两个算法一样用区域码来用区域码测试完成，如果一条线段不能明确接受或者拒绝，则Nicholl-lee-Nicholl算法建立另外的裁剪区域

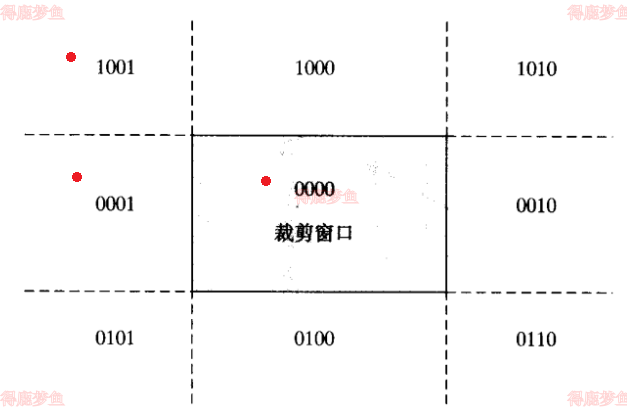
对对于一条线段的线段起点$P_0$和终点$P_2$而言,$P_0$相对于裁剪矩形的九个可能位置如下图所示,我们需要考虑的是红点对应的3个区域，其他的位置都可以通过对称变换将其变换到其中3个区域之中的某一个

$P_0$和$P_1$同时在裁剪区域内

通过梁友栋-barsky线段裁剪算法或者cohen-sutherland线段裁剪算法测试，保留

$P_0$和$P_1$不同时在裁剪区域内

判断$P_1$相对于$P_0$的位置，根据$P_0$的位置在平面上创立新的区域，新区域的边界是以$P_0$为起始点，穿过窗口的顶点的射线，

如果$P_0$在裁剪区域内$P_1$不在裁剪区域内

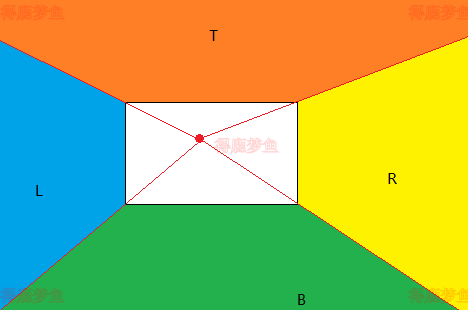
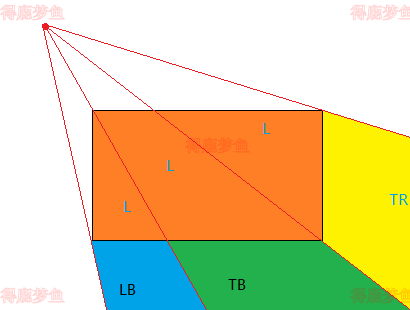
如果$P_0$位于0000区域

设置四个区域，如下图所示，根据$P_1$点的某个一个区域L，T，R，B, 就可以得到线段与窗口的边界

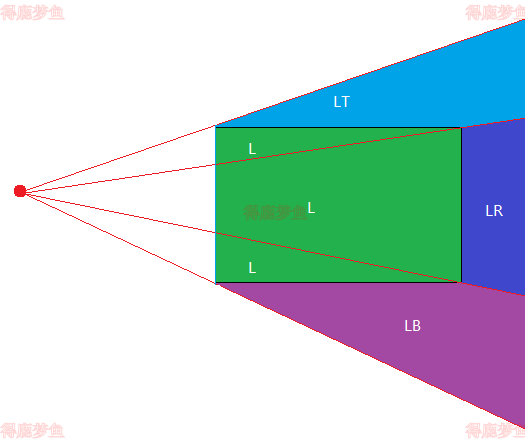
如果$P_0$位于0001区域

设置四个区域，如下图所示，根据$P_1$点的某个一个区域L，LT，LR，LB, 就可以得到线段与窗口的边界

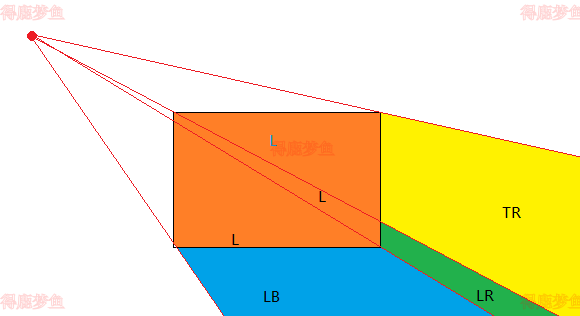
如果$P_0$位于1001区域

设置四个区域，如下图所示

为了确定$P_1$位于那个区域内，要比较该线段的斜率与裁剪边界的斜率

情况一	情况二