cohen-sutherland线段裁剪算法

这是一个最早开发的快速线段裁剪算法，该算法是通过初始测试来减少交点计算，从而减少线段裁剪算法所用的时间，每条线段的端点都被赋以称为区域码的四位二进制码，每一位用来标识端点相对于裁剪矩形边界的里面还是外面，
如下图所示，设定按照右到左的顺序，在这个顺序下，最右边位置对应裁剪窗口的左边界，最左边对应窗口的上边界，任何码位的值为1表示端在在相应窗口边界的外面

每一个裁剪窗口边界将二维空间划分为内部和外部的两个半空间，四个窗口边界一起构成了九个区域

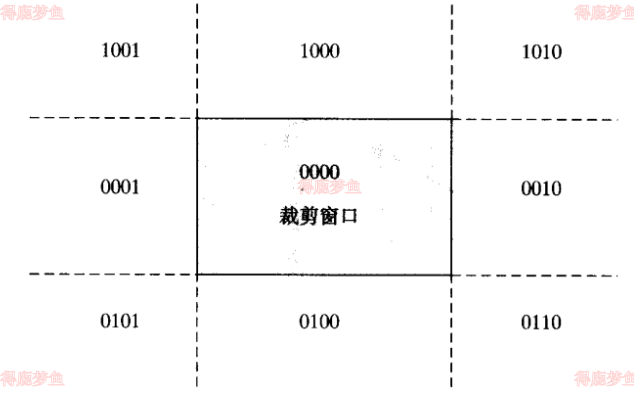
区域码的位值通过将端点的坐标值与裁剪窗口边界相比较而确定，如果$x < xw_{min}$为位置为1，否则为0，其他各位的值于此类似，

按照区域码图的顺序，
第1位为$x - xw_{min}$的符号位
第2位为$xw_{max} - x$的符号位
第3位为$y - yw_{min}$的符号位
第4位为$yw_{max} - y$的符号位

一旦给所有的线段端点建立了区域码，就可以快速的判断那条线端完全在裁剪区域内，那条线完全在裁剪区域外，完全在窗口边界内的端点，

其两个端点的区域码均为0000，也就是逻辑或运算后为0，保留
其两个端点的区域码，有一对相同位置都为1的线段则完全落在裁剪矩形外也就是说逻辑&运算结果不为0，丢弃
对于不能判断为完全在窗口外或者窗口内的线段，则要测试其与窗口边界的交点，可能需要进行多次求交运算才能完成一条线段的裁剪，求交次数依赖与选择裁剪边界的次序，每处理一条裁剪窗口边界后，裁掉其中一部分，剩下部分对照窗口的其余边界进行检测，一直进行到线段完全被裁剪掉或者雨下的线段部分完全 在裁剪窗口内

1. 首先选择一个不完全在窗口边界内的端点，也就是code码不为0b0000的端点
2. 判断该端点在那个区域内，会获取与只对应的交点，替换上述中的所选的端点

示例

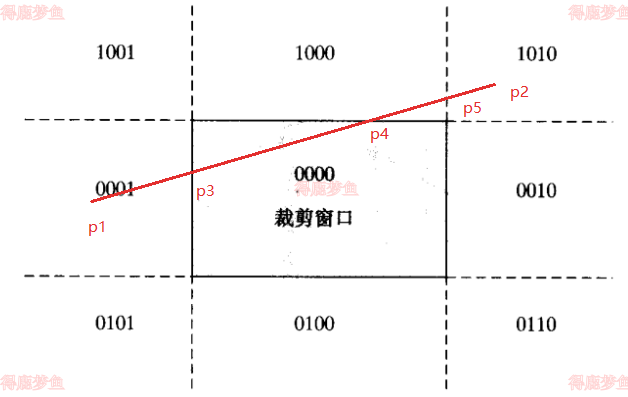
直线与裁剪窗口相交，与p3和p4点，
p1的区域码为0001，p2为1010,都不完全在裁剪窗口内，选择p1为起始点
判断p1和裁剪窗口的相对位置，在左侧区域内，
计算交点p3xmin, y, 使用p3替换p1判断线段的关系p3p2，由于p3的区域码为0000,所以选择p2为判断端点，根据上表中的坐标区域的顺序左右下上，判断出p2在裁剪窗口的右侧，得到交点p5，丢弃p5p2，判断线段p3p5与裁剪窗口的位置，
选择交点p5作为判断点位，p5在裁剪窗口的上侧，，计算p4的位置$x, ymax$ 丢弃p4p5段，剩余p3p4段完全在窗口内完成裁剪，如下图所示

请参考cohen-sutherland线段裁剪算法