得鹿梦鱼 得鹿梦鱼
知识库 前端技能树 面试题 学习资料 关于本人

二维观察

流水线

二维场景中要显示的部分被为裁剪窗口，因为所有在此区域之外的场景均需要裁去，只有在裁剪窗口内部的场景才能显示在屏幕

裁剪窗口和视口一般都是矩形，其各边与坐标轴平行

二维时间坐标系场景描述到设备坐标系的映射被成为二维观察变换，

流水线

裁剪窗口

观察坐标裁剪窗口

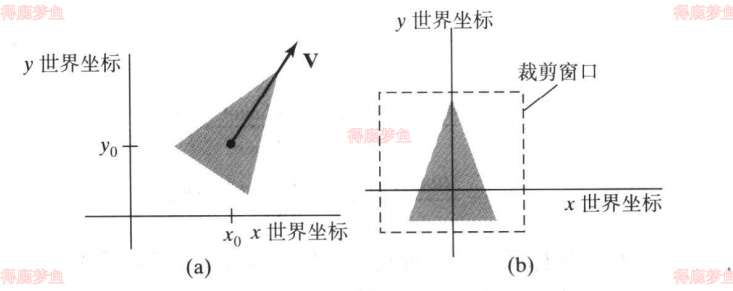
二维观察变换的一般方法是在世界坐标系中指定一个观察坐标系统，以该系统为参考通过选定方向和位置来指定矩形裁剪窗口，如下图所示

观察坐标裁剪窗口

世界坐标系裁剪窗口

我们可以指定世界坐标系中的两点作为标准矩形的两个对角顶点，一旦建立了裁剪窗口，观察函数就对场景描述进行处理并将结果输出到输出设备

世界坐标系裁剪窗口

规范化和视口变换

裁剪窗口到规范化视口的映射

将窗口内的点xw,ywxw,yw映射到对应视口的点xv,yvxv,yv

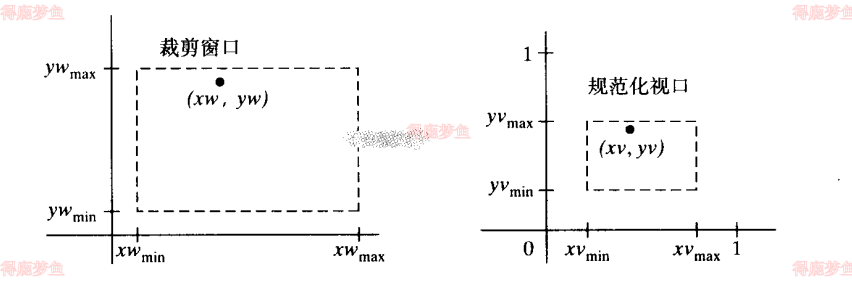
窗口到视口映射

为了满足视口与窗口中的对象具有同样的相对位置，必须满足
{xv−xvminxvmax−xvmin=xw−xwminxwmax−xwminyv−yvminyvmax−yvmin=yw−xwminywmax−ywmin\begin{cases}\frac{xv - xv_{min}}{xv_{max} - xv_{min}} = \frac{xw - xw_{min}}{xw_{max} - xw_{min}} \\\frac{yv - yv_{min}}{yv_{max} - yv_{min}} = \frac{yw - xw_{min}}{yw_{max} - yw_{min}}\end{cases}

求解xv,yvxv,yv

{xv=xvmax−xvminxwmax−xwminxw+xwmaxxvmin−xwminxvmaxxwmax−xwminyv=yvmax−yvminywmax−ywminyw+ywmaxyvmin−ywminyvmaxywmax−ywmin\begin{cases}xv = \frac{xv_{max} - xv_{min}}{xw_{max} - xw_{min}} xw + \frac{xw_{max}xv_{min} - xw_{min}xv_{max}}{xw_{max} - xw_{min}} \\yv = \frac{yv_{max} - yv_{min}}{yw_{max} - yw_{min}} yw + \frac{yw_{max}yv_{min} - yw_{min}yv_{max}}{yw_{max} - yw_{min}}\end{cases}

上式中的变换顺序为

  1. 以点xwmin,xwmaxxw_{min}, xw_{max}为中心执行缩放变换，将窗口变换成视口大小
  2. 将xwmin,xwmaxxw_{min}, xw_{max}移动到xvmin,xvmaxxv_{min}, xv_{max}

矩阵表示为

[sx0xwmin1−sx0syywmin1−sy001][10xvmin−xwmin01yvmin−ywmin001]=[sx0tx0syty001]\begin{bmatrix}s_x & 0 & xw_{min}1-s_x \\0 & s_y & yw_{min}1-s_y \\0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & xv_{min} - xw_{min} \\0 & 1 & yv_{min} - yw_{min} \\0 & 0 & 1\end{bmatrix}\text{=}\begin{bmatrix}s_x & 0 & t_x \\0 & s_y & t_y \\0 & 0 & 1\end{bmatrix}

注意只有在裁剪裁剪窗口和视口有相同的纵横比是才能保持对象的相对比例不变，换句话说，如果缩放因子sx,sys_x,s_y相同，则对象的比例不变，否则世界坐标系中的对象显示到输出设备上时可能在x轴或者y轴方向发生拉伸或者缩短

裁剪窗口到规范化正方形的映射

二维观察的另一种方法是先将裁剪窗口变换到规范化正方形，在规范化坐标系中进行裁剪，然后场景描述变换到屏幕坐标系中指定的视口中，过程上上述一样是，使用xvmin,yvmin=−1xv_{min}, yv_{min} = -1和用xvmax,yvmax=1xv_{max}, yv_{max} = 1代替

字符串的显示

有两种处理方法通过观察流水线将字符串映射到视口上，最简单的映射是保持字符串的大小不变，在使用点阵字体时采用这种方法，但轮廓线字体可以和其他图元一样变换，即只要对字符轮廓中线段的定义位置进行变换，在场景处理中处理过其他图元后对变换后的字符确定像素图案

裁剪算法

一般情况下，任何用来消除指定区域内或者外的图形部分的过程被称为裁剪算法

点的裁剪

设定裁剪窗口是一个在标准位置的矩形，如果点x,yx,y满足下列不等式，则该点显示

{xwmin≤x≤xwmaxywmin≤y≤ywmax\begin{cases}xw_{min} \leq x \leq xw_{max} \\yw_{min} \leq y \leq yw_{max}\end{cases}

线段的裁剪

  1. cohen-sutherland线段裁剪算法
  2. 梁友栋-barsky线段裁剪算法
  3. Nicholl-lee-Nicholl线段裁剪算法

非矩形裁剪窗口的线段裁剪

在某些应用中，需要使用任意形状的多边形对线段进行裁剪，基于参数化直线方程的算法，如cohen-sutherland线段裁剪算法和梁友栋-barsky线段裁剪算法都可以扩充到凸多边形窗口，只需修改算法使参数化方程适合裁剪区域的边界即可

对于凹多边形，可以考虑先将凹多边形转化为凸多边形后再进行上述的裁剪
可以参考

  1. 一种凹多边形凸分解的全局剖分算法
  2. 一个加权剖分简单多边形为凸多边形的算法
  3. 改进的加权剖分简单多边形为凸多边形的算法

多边形填充区的裁剪

为了裁剪一个填充多边形，不能直接使用线裁剪算法对多边形的每一条边进行裁剪，因为该方法一般能生成封闭的折线，相反使用线段裁剪算法进行处理的多边形边界会显示会一系列不连接的线段，并且没有如何形成裁剪后的封闭边界信息

  1. Sutherland-Hodgman多边形裁剪算法
  2. weiler-Atherton多边形裁剪算法

曲线的裁剪

可以先测试对象与裁剪窗口坐标范围来确定是否可以简单的接受或者拒绝整个对象，如果不能，则再检查对称性来确是否可以简单的接受或者拒绝，
利用一般的多边形裁剪窗口对曲线对象的裁剪可使用类似的方法，第一轮，比较对象包围矩形和裁剪窗口的包围盒，如果不能保存和排除整个对象，则接着求解直线-曲线联立方程来确定裁剪交点

文字的裁剪

第一种方法全部保留或者全部舍弃字符串的裁剪策略；如果字符串中所有字符都在裁剪窗口内，那么就全部保留这些内容，否则舍弃，通过测试字符串的坐标范围来实现
第二种方法使用全部保留或者全部舍弃字符的策略，这里仅舍弃并没有完全落在裁剪窗口内的字符，这这种情况下，每一个字符的边界要与窗口进行比较，任何没有完全落在裁剪窗口内的字符都要被裁剪
第三种方法是裁剪单个字符的部分，提供了裁剪后字符串的最精确的显示，但是需要较多的时间处理，如果一个字符与裁剪窗口边界有重叠，则裁掉位于窗口之外的字符部分

二维观察
≡