空间分析
主要内容
从宏观上划分,空间分析可以归纳为以下三个方面:
- 拓扑分析 包括空间图形数据的拓扑运算,即旋转变换、比例尺变换、三维及三维显示、几何元素计算等。
- 属性分析 包括数据检索、逻辑与数学运算、重分类、统计分析等。
- 拓扑与属性的联合分析 包括与拓扑相关的数据检索、叠置处理、区域分析、邻域分析、 网络分析 、形状探测、 瘦化处理、空间内插等。
步骤
- 建立分析的目的和标准
- 准备空间操作的数据
- 进行空间操作
- 准备表格分析的数据
- 进行表格分析
- 对结果进行评价
- 如果必要,改进分析
- 输出最终的结果和报告
空间度量算法
长度量算
- 2点之间的距离
d2=x2−x12+y2−y12
d3=x2−x12+y2−y12+z2−z12
- 点到直线的距离
2.1 两点定义的直线
在二维和三维中,当L是通过两个点P0,P1给出的,我们可以使用矢量积直接计算出点P到L的距离,两个矢量的矢量积的模等于两个矢量构成的平行四边形的面积,即:v×w=∣v∣∣w∣sinθ,其中θ是两个矢量之间的夹角。
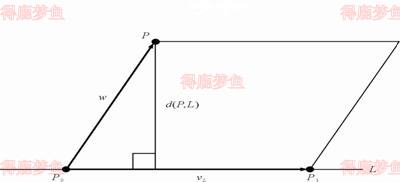
dP,L=∣vl∣v×w∣=∣vl×w∣
2.2 二维隐式方程定义的直线
在二维中,有许多情况下,直线L是很容易通过一个隐式方程来定义fx,y=ax+by+c=0。 对于任意二维点P=x,y、距离dP,L可以直接用这个方程计算出
矢量nL=a,b是直线L的法线矢量,利用nL我们可以计算任意点P到L的距离。 首先在L上任意选一点P0,然后将矢量P0P投影到nL
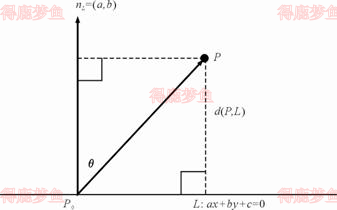
dP,L=a2+b2ax+by+c
2.3 参数方程定义的直线
在n维空间中,已知直线L的参数方程为Pt=P0+tP1−P0,P为任意n维空间中的任意一点。 为了计算点P到直线L的距离dP,L,从点P作直线L的垂线,交于点Pb。 则向量P0Pb是矢量P0P在线段P0P1上的投影,如下图
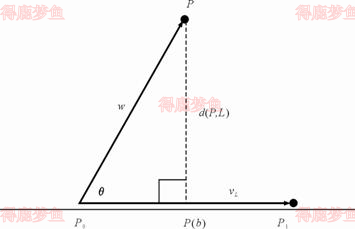
b=dP0,P1dP0,Pb=∣vl∣∣w∣cosθ=∣vl∣2w−vl=vl⋅v∣w⋅vl
dP,L=∣∣P−Pb∣=∣w−bvl∣=w−w⋅vlvl
角度度量
求直线a0x+b0y+c=0与直线a1x+b1y+c=0的夹角公式
tanθ=a0a1+b0b1a0b1−a1b0
当分子为零时则两直线平行
当分母为零时则两直线垂直
面积量算
矢量数据多边形的面积计算基于求三角形面积之和的原理,即多边形面积等于其内部所有三角形的面积和。
分布中心
- 算数平均中心
- 加权平均中心:
- 中位中心:中位中心是指到各个离散点距离和为最小的一个点
- 极值中心:极值中心是指到各个离散点中最大距离为最小的一个点
