地图投影的选择
地图投影是将地球椭球面上的地理信息，科学、准确地转绘到平面上的控制骨架和定位依据
影响因素
- 制图区域的地理位置，形状和范围
制图区域的地理位置决定了所选择投影的种类。例如，制图区域在极地位置，可选择正轴方位投影；制图区域在赤道附近，应考虑选择横轴方位投影或正轴圆柱投影；若制图区域在中纬地区，则应考虑选择正轴圆锥投影或斜轴方位投影
根据制图区域的形状选择投影时，应遵循一条基本原则：投影的无变形点和线应位于制图区域的中心位置，等变形线尽量与制图区域的形状一致，从而保证制图区域的变形分布均匀。
制图区域的范围大小也影响地图投影的选择。当制图区域范围不太大时，无论选择什么投影，制图区域内各处变形差异都不会太大
地图的内容
地图所表现的主题和内容是什么，关系到选择什么投影。如交通图、航海图、航空图、军用等方面的地图，要求方向正确，小区域的形状能与实地相似，应选择等角投影。而自然地图和社会经济地图中的分布图、类型图、区划图等则要求保持面积对比关系的正确，因此应选用等积投影。再如世界时区图，为了使时区的划分表现的清楚，只能选择经线投影成直线的正轴圆柱投影出版方式
地图在出版方式上，有单幅图、系列图和地图集之分。单幅图的投影选择比较简单，只考虑上述几个原则即可；系列图虽然表现内容较多，但由于性质相近，也应该选择同一变形性质的投影，以便于相互比较与参证，而地图集，情况就比较复杂了。由于图集是一个统一协调的有机整体，故投影选择又不能过多，应尽量采用同一系统的投影，再根据个别内容的特殊要求，在变形性质方面予以适当变化。
国内GIS中地图投影的应用
我国的各种地理信息系统中都采用了与我国基本比例尺地形图系列一致的地图投影系统，这就是大于等于1∶50万时采用高斯—克吕格投影，1∶100万采用正轴等角割圆锥投影
我国基本比例尺地形图1∶5千，1∶1万，1∶2.5万，1∶5万，1∶10万，1∶25万，1∶50万和1∶100万中大于等于1∶50万的图均采用高斯—克吕格投影为地理基础；
我国1∶100万地形图采用正轴等角割圆锥投影，其分幅与国际百万分之一所采用的分幅一致
我国大部分省区图多采用正轴等角割圆锥投影和属于同一投影系统的正轴等面积割圆锥投影
正轴等角圆锥投影中，地球表面上两点间的最短距离即大圆航线表现为近于直线，这有利于地理信息系统中空间分析和信息量度的正确实施
高斯—克吕格投影
概念
高斯投影从几何概念上分析，它是一种等角横切椭圆柱投影。我们把地球看成是地球椭球体，假想用一个椭圆筒横套在其上，使筒与地球椭球体的某一经线相切，椭圆筒的中心轴位于赤道上，按等角条件将地球表面投影到椭圆筒上，然后将椭圆筒展开成平面
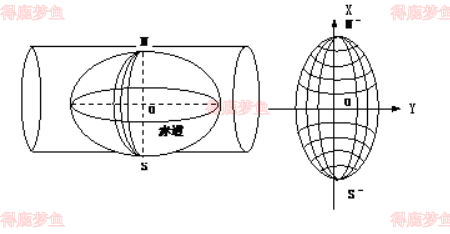
基本条件
中央经线椭圆筒和地球椭球体的切线和赤道投影成垂直相交的直线
投影后没有角度变形即经纬线投影后仍正交
中央经线上没有长度变形，等变形线为平行于中央经线的直线
平面直角坐标系的纵、横坐标
椭球面上地理坐标系的经纬度
s 由赤道至纬度的子午线弧长；
N 纬度处的卯酉圈曲率半径
; a，b分别为地球椭球体的长短轴
正轴等角圆锥投影
定义
假想一个圆锥其轴与地球椭球旋转轴重合地套在椭球上，按等角的条件把地球椭球上经纬线投影到圆锥面上，然后沿一条母线经线将圆锥面切开展成平面，这就是正轴等角圆锥投影。
圆锥面与椭球面相割的两条纬线圈，称之为标准纬线φ1，φ2。采用双标准纬线的相割比采用单标准纬线的相切，其投影变形小而均匀
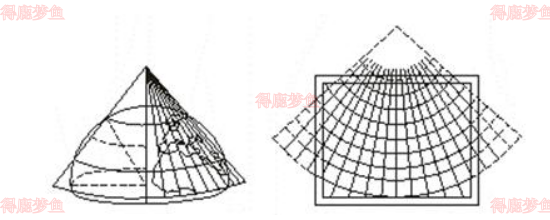
投影变形
角度没有变形，即投影前后对应的微分面积保持图形相似
等变形线和纬线一致，同一条纬线上的变形处处相等
两条标准纬线上没有任何变形
在同一经线上，两标准纬线外侧为正变形长度比大于1，而两标准纬线之间为负变形长度比小于1。因此，变形比较均匀，绝对值也比较小
同一纬线上等经差的线段长度相等，两条纬线间的经纬线长度处处相等