得鹿梦鱼 得鹿梦鱼
知识库 前端技能树 面试题 学习资料 关于本人

基本问题

是如何将地球表面椭球面或圆球面表示到地图平面上。由于地球椭球面或圆球面是不可展开的曲面，即不能展开成平面，而地图又必须是一个平面，所以将地球表面展开成地图平面必然会产生裂隙或褶皱；那么采用什么样的数学方法将曲面展开成平面，而使其误差最小，必须采用地图投影的方法，即用各种方法将地球表面的经纬网线投影到地图平面上。

地图投影

定义：建立地球椭球表面或球体表面与地图平面之间点与点或线与线之间的一一对应关系
{X=f1φ,γY=f2φ,γ\begin{cases}X = f_{1}\varphi,\gamma \\Y = f_{2}\varphi,\gamma\end{cases}

地图投影的变形

地球表面是一个不规则的曲面，即使把它当作一个椭球体或正球体表面，在数学上讲，它也是一种不能展开的曲面，要把这样一个曲面表现到平面上，就会发生裂隙或褶皱。在投影面上，则以经纬线的“拉伸”或“压缩”通过数学手段来避免之，从而可形成一幅完整的地图，也就因此而产生了变形。地图投影的变形，通常可分为长度、面积和角度三种变形，

长度比——地面上微分线段投影后的长度ds′与其相应的实地长度ds之比 μ=ds′ds\mu = \frac{ds′}{ds}

长度变形——长度比与1之差值。如用符号Vμ表示长度变形 Vμ=μ−1V\mu = \mu - 1

投影上的长度比不仅随该点的位置而变换，而且随着在该点上不同方向而变化，这样。在一定点上的长度比存在最大值和最小值，被称为极值长度比，并通常用符号a和b表示极大与极小长度比。极值长度比的方向称为主方向。沿经线和纬线方向的长度比分别用符号m，n表示。在经纬线正交投影中，沿经纬线方向的长度比即为极值长度比，此时m=a或 b，n=b或a。

面积比——地面上微分面积投影后的大小dF′与其相应的实地面积dF的比称为面积比，通常用符号P表示P=dF′dFP=\frac{dF′}{dF}

面积变形——面积比与1之差值。用符号Vp表示Vp=P−1Vp = P - 1

角度变形——地面上某一角度投影后的角值β′\beta′与其实际的角值β\beta之差。即β′−β\beta′- \beta。在一定点上，方位角的变形随不同的方向而变化，所以一点上不同方向的角度变形是不同的。投影中，一定点上的角度变形的大小是用其最大值来衡量的，即称最大角度变形，通常用符号ω表示

变形椭圆——地球面上无穷小圆在投影中通常不可能保持原来的形状和大小，而是投影成为不同大小的圆或各种形状大小的椭圆，统称为变形椭圆

变形椭圆类型
a=b：该投影为等角投影
a·b=r2r^2：该投影为等面积投影
任意投影：投影后为面积不等形状各不相同的椭圆
b=r: 为等距离投影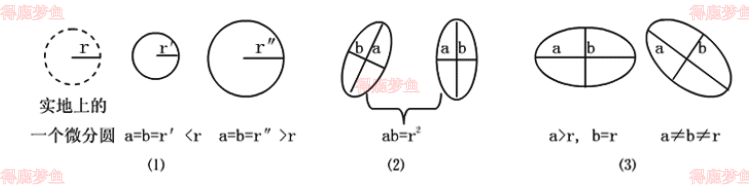
变形椭圆

分类

地图投影的变形内蕴的特征分类

  1. 等角投影
    地球表面上无穷小图形投影后仍保持相似，或两微分线段所组成的角度在投影后仍保持相似，或两微分线段所组成的角度在投影后仍保持不变，这种投影称等角投影又称正形投影。
  2. 等面积投影
    在等面积投影中，微分圆变成不同形状的椭圆，但变形椭圆面积保持相等，只有角度产生很大变形
  3. 任意投影
    既不具备等角性质，又没有等面积性质的投影

投影面与地球表面的相关位置分类

我们首先将不可展的椭球面投影到一个可展曲面上，然后将该曲面展开成为一个平面，得到我们所需要的投影。通常采用的这个可展曲面有圆锥面、圆柱面、平面曲率为零的曲面，相应地可以得到圆锥投影、圆柱投影、方位投影。同时还可以由投影面与地理轴向的相对位置区分为正轴投影极点在两地极上，或投影面的中心线与地轴一致、横轴投影极点在赤道上，或投影面的中心线与地轴垂直及斜轴投影极点既不在两地极上又不在赤道上，或投影面的中心线与地轴斜交。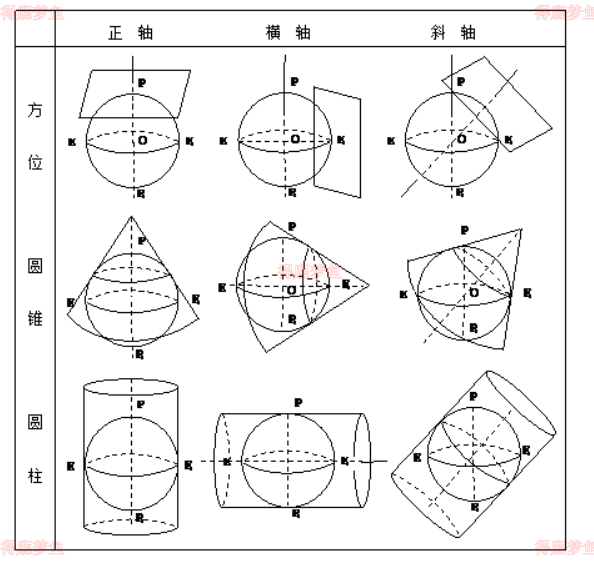
投影方法

正轴投影时经纬网的形状分类

跟据这一标志，投影可分为圆锥、圆柱、方位、伪圆锥、伪圆柱、伪方位和多圆锥投影等

  1. 圆锥投影
    投影中纬线为同心圆圆弧，经线为圆的半径，且经纬间的夹角与经差成正比例
    该投影按变形性质又可分为等角、等面积和任意主要为等距离圆锥投影。等角圆锥投影也称为兰勃特Lambert正形圆锥投影；正轴等面积割圆锥投影亦叫亚尔勃斯Albers投影

  2. 圆柱投影
    投影中纬线为一组平行直线，经线为垂直于纬线的另一组平行直线，且两相邻经线之间的距离相等
    该投影按变形性质可分为等角、等面积和任意包括等距离圆柱投影。等角圆柱投影亦叫墨卡托Mercator投影，它在海图和小比例尺区域地图上有广泛应用。等角横切椭圆柱投影，即著名的高斯—克吕格Gauss-kruger投影，等角横割椭圆柱投影即通用横轴墨卡托UTM投影，它们都广泛用于编制大比例尺地形图

3.方位投影
投影中纬线为同心圆，经线为圆的半径，且经线间的夹角等于地球面上相应的经差
该投影有非透视方位投影和透视方位投影之分。非透视方位投影按变形性质可分为等角、等面积和任意包括等距离方位投影。等面积方位投影亦称为兰勃特Lambert等面积方位投影。等距离方位投影又称为波斯托Postel投影

  1. 伪圆锥投影
    投影中纬线为同心圆圆弧，经线为交于圆心的曲线

  2. 伪圆柱投影

投影中纬线为一组平行直线，而经线为某种曲线
6. 伪方位投影

投影中纬线为同心圆，而经线为交于圆心的曲线
7. 多圆锥投影

投影中纬线为同轴圆圆弧，其圆心在中央直径线上，而经线为对称中央直径线的曲线

地图投影与GIS的关系

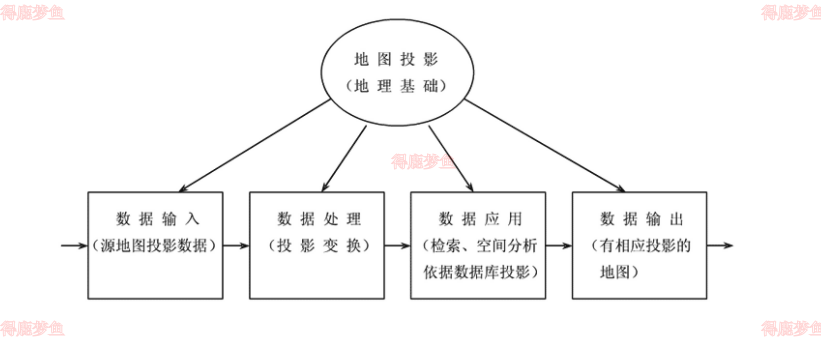
地图投影与GIS的关系

GIS中地图投影的配置与设计

  1. 所配置的投影系统应与相应比例尺的国家基本图基本比例尺地形图、基本省区图或国家大地图集投影系统一致
  2. 系统一般最多只采用两种投影系统，一种服务于大比例尺的数据处理与输入输出， 另一种服务于中小比例尺
  3. 所用投影以等角投影为宜
  4. 所用投影应能与网格坐标系统相适应，即所用的网格系统在投影带中应保持完整

基本问题

地图投影的变形

分类

地图投影与GIS的关系

GIS中地图投影的配置与设计

≡