矩阵的初等变换与线性方程组
矩阵的初等变换
初等行变换
- 对调两行
- 数k=0乘某一行中的所有元素
- 把某一行的所有元素的k倍加到另一行对应的元素上
初等列变换
- 对调两列
- 数k=0乘某一列中的所有元素
- 把某一列的所有元素的k倍加到另一列对应的元素上
矩阵的初等行变换和初等列变换统称为初等变换
如果矩阵A经过有限次初等行变换变成矩阵B,称矩阵A和矩阵B行等阶
如果矩阵A经过有限次初等列变换变成矩阵B,称矩阵A和矩阵B列等阶
如果矩阵A经过有限次初等变换变成矩阵B,称矩阵A和矩阵B等阶 A ~ B
等价的性质
- 反身性 A ~ A
- 对称性 若A ~ B则B ~ A
- 传递性 若A ~ B, B ~ C则A ~ C
行阶梯矩阵
可以画出一条阶梯线,线的下方全部为0,每个台阶只有一行,台阶数既是非零行的行数,阶梯线的竖线后面的第一个元素为非零元,也就是非零行的第一个非零元
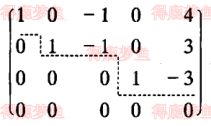
行最简形矩阵
非零行的第一个非零元为1,且这些非零元所在列的其他元素均为0
解线性方程组的解只需要把增广矩阵化为行最简形矩阵
标准形
对行最简矩阵在施以初等列变换,可以变成一种形态更加简单的矩阵,称为标准形,特点是左上角是一个单位矩阵,其余元素均为0
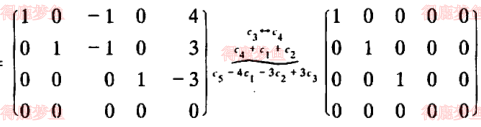
设A, B为m×n矩阵则
定理1:A ~ B的充要条件是存在m阶可逆矩阵使得PA=B
定理2:A ~ B的充要条件是存在n阶可逆矩阵使得AQ=B
定理3:A ~ B的充要条件是存在M阶可逆矩阵以及n阶可逆矩阵使得PAQ=B
由单位矩阵经过一次初等变换后得到的矩阵叫做初等矩阵
设A为m×n矩阵
性质1: 对A执行一次初等行变换相当于在A的左边乘以相应的m阶初等矩阵
性质2: 对A执行一次初等列变换相当于在A的右边乘以相应的m阶初等矩阵
性质3: 方阵A可逆的充要条件是存在有限个初等矩阵,使得A=P1P2...Pm
