向量组及其线性组合
向量
既有大小又有方向的量被称为向量
只有大小没有方向的量被称为标量
数学上用一条有方向的线段表示向量,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向,a
向量的大小称为向量的模或者长度,也称为向量的范数,记作 ∣a∣
模长为 1 的向量称为单位向量,记作e
模长为 0 的向量称为零向量,记作0,规定零向量的方向是任意的
向量相等:两向量的大小相等、方向相同,不论起点是否相同,记作a=b
定义 1: n 个有次序的数a1,a2,...,an所组成的数组叫做 n 维向量,这 n 个数叫做 n 维向量的 n 个分量
n 维向量可以写成一行或者一列,按照矩阵的规定,分别被称为行向量和列向量, 行向量和列向量互为转置矩阵
向量的加减法
如果向量a=OA与b=OB在同一直线上,那么,规定它们的和是这样的一个向量:
当OA和OB的方向相同时,和的方向与原来的两向量相同,其模等于两向量的模之和,当OA和OB的方向相反时,其模等于两向量的模之差,其方向与模值大的向量方向一致,对于其他的向量采用平行四边形法则
向量加法满足一下运算规律:
- 交换律:a+b=b+a
- 结合律:a+b+c=a+b+c=a+b+c
与a的模相同而方向相反的向量被称为 a 的负向量,记作−a,规定两个向量的差为向量a+−b=a−b,记作向量的减法
特别地: a−a=a+−a=0
向量与数的乘法
对任意的实数λ与向量a,可定义a与λ的乘积(简称数乘)为一向量,记作λa, 它的模与方向规定如下
- ∣λa∣=∣λ∣⋅∣a∣
- 当λ>0是,向量λa∣的方向与a的方向相同,当λ<0是,向量λa∣的方向与a的方向相反,当λ=0是,向量lambdaa=0
数乘满足一下运算规律
- 结合律: λμa=λμa=λμa
- 分配律:λ+μa=λa+μa,λa+b=λa+λb
几何中,“空间”通常是作为点的集合,即作为“空间”的元素是点,这样的空间叫做点空间
我们把三维向量的全部所组成的集合R3={r=x,y,zT∣x,y,z∈R}叫做三维向量空间
若干个同维数的列向量所组成的集合叫做向量组
本文中规定向量默认使用列向量,用行向量表示其转置
a1,a2,...,an
a1a2...an
向量的线性运算
定义2: 给定向量组A:a1,a2,...,an,对于任意一组实数k1,k2,...,kn满足表达式
k1a1+k2a2+...+knan
称为向量组的一个线性空间,k1,k2,...,kn叫做线性组合的系数
给定向量组A:a1,a2,...,an,和向量b,如果存在一组实数λ1,λ2,...,λn满足下式
b=λ1a1+λ2a2+...+λnan
则向量b是向量组 A 的线性组合,也称向量b能有向量组A线性表示
向量的线性相关性
额
如果n=2,其几何意义是两向量共线,
如果n=3,其几何意义是三向量共面
定理 1: 设向量a=0,那么向量a∥平行b的充要条件是:存在唯一的实数λ使得b=λa
定理 2: 三个非零向量a,b,c共面的充分必要条件是其中一个向量可以表示成其余两个向量的线性组合
向量的秩
定义4:设有向量组A,如果在A中能选出r个向量a1,a2,...,ar,满足
- 向量组A0:a1,a2,...,ar线性无关
- 向量组A中任意r+1(如果存在)个向量都线性有关
那么向量组A0是向量组A的一个最大线性无关向量组,最大无关组所含向量个数为向量的秩,记作RA
只含有零向量的向量组没有最大无关组,规定秩为零
向量空间
设V为n维向量的集合,如果集合V非空,且集合V对于向量的加法以及数乘两种运算封闭,那么就成集合V为向量空间
封闭:是指在集合中可以进行向量的加法和数乘两种运算
点的坐标与向量的坐标
空间直角坐标系
过空间一定点 O,做三条互相垂直的数轴,他们都是以 O 为原点,且具有相同的长度单位,这三条轴分别叫做 x 轴,y 轴,z 轴,且统称为坐标轴
三条坐标轴中的任意两条可以确定一个平面,这样就定出的三个平面统称为坐标面,将空间分成了八个部分,每个部分被分为一个卦限
向量的坐标表示
在空间直角坐标系 Oxyz 中,称沿 x 轴,y 轴,z 轴正向的单位向量为 Oxyz 坐标系下的标准单位向量,分别记为i,j,k,对于任意向量a,总可平移使其起点位于坐标原点,从而存在对应点 M,满足OM=a,以 OM 为对角线作长方体,设点在 x 轴,Y 轴,z 轴上的投影点为 P,Q,R,如下图:
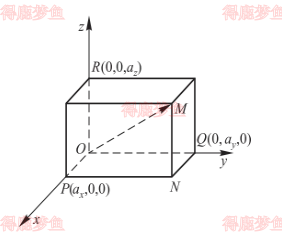
则存在a=OM=OP+PN+NM=OP+OQ+OR
设点 P,Q,R 在 x 轴,y 轴,z 轴上的坐标分别为ax,ay,az则
OP=axi,OQ=ayj,OR=azk
a=axi+ayj+azk
上式表示空间任一向量a可以表示为标准单位向量i,j,k的线性组合,我们也称上式为向量a的标准分解式,其中axi,ayj,azk为向量a沿三条坐标轴方向的分向量。
由定理 2 得,三个向量a,b,c共面的充要条件是存在不全为 0 的数k1,k2,k3使得k1a+k2b+k3c=0
用向量的坐标表示上述关系,即
⎩⎨⎧k1ax+k2ax+k3ax=0k1ay+k2ay+k3ay=0k1az+k2az+k3az=0
这是一个关于未知量k1,k2,k3的其次线性方程组,他有非零解,故此线性方程组的系数行列式为零,从而由如下定理:
定理 3 三个向量a=ax,ay,az,b=bx,aby,bz,c=cx,cy,cz共面的充要条件
axbxcxaybycyazbzcz=0
向量的模、方向角
向量可以用它的模与方向来表示,也可以用它的坐标来表示,而且向量的这两种表示法之间有着密切的联系,事实上,向量的模与方向都可以用它的坐标来表示。
向量的模∣a∣=ax2+ay2+az2
如下图所示,设非零向量a与三条坐标轴的正向的夹角,即与标准单位向量i,j,k的夹角分别为α,β,γ,称为向量的方向角,方向角的余弦称为向量的方向余弦。
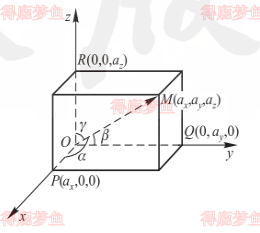
⎩⎨⎧cosα=∣a∣ax=ax2+ay2+az2axcosβ=∣a∣ay=ax2+ay2+az2axcosγ=∣a∣az=ax2+ay2+az2ax
且满足关系式cos2α+cos2β+cos2γ=1
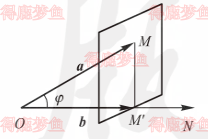
向量的投影
设向量a=OM,b=ON,且b=0,a和b的夹角为φ,过点 M 作平面垂直于 b 所在的直线并交直线与点 M',则称有向线段为a在b上的投影向量,如下图