得鹿梦鱼 得鹿梦鱼
知识库 前端技能树 面试题 学习资料 关于本人

向量代数与空间解析几何

向量及其线性运算

既有大小又有方向的量被称为向量
只有大小没有方向的量被称为标量

数学上用一条有方向的线段表示向量，有向线段的长度表示向量的大小，有向线段的方向表示向量的方向，a→\overrightarrow a

有些向量与其起点无关，对于一切向量的共性是他们都有大小和方向，因此在数学上只研究与起点无关的向量，并称这种向量为自由向量

向量相等：两向量的大小相等、方向相同，不论起点是否相同，记作a→=b→\overrightarrow a = \overrightarrow b,换句话说就是经过平移移动后能够完全重合的向量是相等的

向量的大小叫做向量的模，记作∣a→∣\overrightarrow a
模长为1的向量称为单位向量，模长等于零的向量叫做零向量

注1零向量的方向是任意的

设存在两个非零向量a→,b→\overrightarrow a,\overrightarrow b,任取空间一点O，作OA→=a→,OB→=b→\overrightarrow{OA} = \overrightarrow a, \overrightarrow{OB} = \overrightarrow b,规定不超过π\pi的∠AOB\angle{AOB}成为向量a→,b→\overrightarrow a,\overrightarrow b的夹角

  1. 向量a→,b→\overrightarrow a,\overrightarrow b的夹角为0或者π\pi 向量a→,b→\overrightarrow a,\overrightarrow b平行、
  2. 向量a→,b→\overrightarrow a,\overrightarrow b的夹角为π2\frac{\pi}{2}向量a→,b→\overrightarrow a,\overrightarrow b垂直

向量的线性运算

向量的加减法

三角性法则或者平行四边形法则

向量加法满足一下运算规律：

  1. 交换律：a→+b→=b→+a→\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a
  2. 结合律：a→+b→+c→=a→+b→+c→=a→+b→+c→\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow a + \overrightarrow b + \overrightarrow c= \overrightarrow a + \overrightarrow b + \overrightarrow c

与a→\overrightarrow a的模相同而方向相反的向量被称为 a 的负向量，记作−a→-\overrightarrow a,规定两个向量的差为向量a→+−b→=a→−b→\overrightarrow a + -\overrightarrow b = \overrightarrow a - \overrightarrow b,记作向量的减法

向量与数的乘法

对任意的实数λ\lambda与向量a→\overrightarrow a,可定义a→\overrightarrow a与λ\lambda的乘积（简称数乘）为一向量，记作λa→\lambda \overrightarrow a, 它的模与方向规定如下

  1. ∣λa→∣=∣λ∣⋅∣a→∣\lambda \overrightarrow a = \lambda \cdot \overrightarrow a
  2. 当λ>0\lambda > 0是，向量λa→∣\lambda \overrightarrow a的方向与a→\overrightarrow a的方向相同，当λ<0\lambda < 0是，向量λa→∣\lambda \overrightarrow a的方向与a→\overrightarrow a的方向相反，当λ=0\lambda = 0是，向量lambdaa→=0→lambda \overrightarrow a = \overrightarrow 0

数乘满足一下运算规律

  1. 结合律： λμa→=λμa→=λμa→\lambda \mu \overrightarrow a = \lambda \mu \overrightarrow a =\lambda \mu \overrightarrow a
  2. 分配律：λ+μa→=λa→+μa→,λa→+b→=λa→+λb→\lambda + \mu\overrightarrow a = \lambda \overrightarrow a + \mu \overrightarrow a, \lambda \overrightarrow a + \overrightarrow b = \lambda \overrightarrow a + \lambda \overrightarrow b

空间直角坐标系

过空间一定点 O,做三条互相垂直的数轴，他们都是以 O 为原点，且具有相同的长度单位，这三条轴分别叫做 x 轴，y 轴，z 轴，且统称为坐标轴
三条坐标轴中的任意两条可以确定一个平面，这样就定出的三个平面统称为坐标面，将空间分成了八个部分，每个部分被分为一个卦限

向量的坐标表示

在空间直角坐标系 Oxyz 中，称沿 x 轴，y 轴，z 轴正向的单位向量为 Oxyz 坐标系下的标准单位向量，分别记为i→,j→,k→\overrightarrow i, \overrightarrow j, \overrightarrow k,对于任意向量a→\overrightarrow a,总可平移使其起点位于坐标原点，从而存在对应点 M，满足OM→=a→\overrightarrow{OM}=\overrightarrow a,以 OM 为对角线作长方体，设点在 x 轴，Y 轴，z 轴上的投影点为 P,Q,R，如下图：
点投影
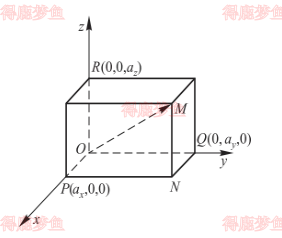
则存在a→=OM→=OP→+PN→+NM→=OP→+OQ→+OR→\overrightarrow a = \overrightarrow{OM}=\overrightarrow{OP}+\overrightarrow{PN}+\overrightarrow{NM} = \overrightarrow{OP} + \overrightarrow{OQ} + \overrightarrow{OR}
设点 P,Q,R 在 x 轴，y 轴，z 轴上的坐标分别为ax,ay,aza_x, a_y, a_z则

OP→=axi→,OQ→=ayj→,OR→=azk→\overrightarrow{OP} = a_x\overrightarrow i ,\overrightarrow{OQ} = a_y\overrightarrow j ,\overrightarrow{OR} = a_z\overrightarrow k

a→=axi→+ayj→+azk→\overrightarrow a = a_x\overrightarrow i + a_y\overrightarrow j + a_z\overrightarrow k

数量积、向量积以及混合积

设a→,b→\overrightarrow a, \overrightarrow b是两向量，且他们之间的夹角为θ\theta,称数∣a→∣⋅∣b→∣cosθ\overrightarrow a \cdot \overrightarrow b cos \theta为向量的数量积，记作a→⋅b→=∣a→∣⋅∣b→∣cosθ\overrightarrow a \cdot \overrightarrow b =\overrightarrow a \cdot \overrightarrow b cos \theta向量的数量积也称为向量的点积或者内积

设a→,b→\overrightarrow a, \overrightarrow b是两向量， 规定两向量的向量积为一向量，记作a→×b→\overrightarrow a \times \overrightarrow b,它的模与方向分别为

  1. 模长： ∣a→×b→∣=∣a→∣∣b→∣sinθ\overrightarrow a \times \overrightarrow b = \overrightarrow a\overrightarrow bsin \theta
  2. 方向: a→×b→\overrightarrow a \times \overrightarrow b,同时垂直于a→\overrightarrow a, b→\overrightarrow b且3个向量满足右手规则，

向量的向量积又被称为叉积或者外积

设已知三个向量a→,b→,c→\overrightarrow a, \overrightarrow b, \overrightarrow c,先做两向量a→,b→\overrightarrow a,\overrightarrow b的向量积，然后在第三个向量c→\overrightarrow c在做数量积，这样得到的数量叫做三向量的a→,b→,c→\overrightarrow a, \overrightarrow b, \overrightarrow c的混合积，记作[abc][abc]

平面

  1. 若点Mx,y,z在曲面Z上，则M的坐标满足方程Fx,y,z = 0
  2. 若一组数x,y,z满足方程Fx,y,z = 0,则点在曲面Z上

则称Fx,y,z = 0为曲面Z的方程，曲面Z为方程Fx,y,z = 0的图形

平面的方程

点法式方程

若一个非零向量垂直与一平面，则称此向量是该平面的法向量， 显然，平面上的任一向量都与此平面的法向量垂直，由于过空间中一点可以做而且只能作一平面垂直于已知直线，因此，当给定平面π\pi上一点M0x0,y0,z0M_0x_0,y_0,z_0和它的一个法向量nA,B,C\bold nA,B,C后，平面的位置就确定了Ax−x0+By−y0+Cz−z0=0Ax-x_0 +By - y_0 + Cz-z_0 =0

一般方程

Ax+By+Cz+D=0Ax + By + Cz + D = 0

点到平面的距离

d=∣Ax0+By0+Cz0+D∣A2+B2+C2d = \frac{Ax_0 + By_0 + Cz_0 + D}{\sqrt{A^2 + B^2 + C^2}}

两平面的位置关系

两平面的夹角：两平面的法向量的夹角被称为两平面的夹角（通常不取钝角）
cosθ=∣n1⋅n2∣n1∣⋅∣n2∣∣=∣A1A2+B1B2+C1C2∣A12+B12+C12A22+B22+C22cos \theta = \frac{\bold n_1 \cdot \bold n_2}{\bold n_1\cdot\bold n_2} = \frac{A_1A_2 + B_1B_2 + C_1C_2}{\sqrt{A_1^2 + B_1^2 + C_1^2}\sqrt{A_2^2 + B_2^2 + C_2^2}}

向量代数与空间解析几何
≡