微分中值定理

中值定理

罗尔定理

费马引理： 设函数$fx$在点$x_0$的某领域$ux_0$内有定义，并且在$x_0$处可导，如果对任意的$x \in ux_0$有$fx \leq fx_0$或者$fx \geq fx_0$$,那么$f'x_0 = 0$

通常称导数为零的点为函数的额驻点（稳定点或者临界点）

罗尔定理： 如果函数$fx$满足

1. 在闭区间$[a,b]$上连续
2. 在开区间$a,b$上可导
3. 在区间端点处的函数值相等，即$fa = fb$
   那么在$a,b$内至少有一点$\xi$, 使得$f'\xi = 0$

拉格朗日中值定理中值定理

拉格朗日中值定理：如果函数$fx$满足

1. 在闭区间$[a,b]$上连续
2. 在开区间$a,b$上可导

那么在$a,b$内至少有一点$\xi$, 使得$fb - fa= f'\xib-a$

罗尔定理和拉格朗日中值的几何意义

	罗尔定理	拉格朗日中值定理
函数图像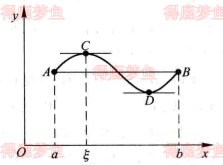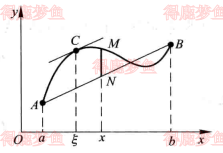
几何意义	弧上至少有一点使得C处的切线平行于x轴	弧上至少有一点使得C处的切线平行于弦AB

定理： 如果函数$fx$在区间I上连续，可导且导数恒为零，那么$fx$在区间I上是一个常数

柯西中值定理

柯西中值定理：如果函数$fx$以及$Fx$满足

1. 在闭区间$[a,b]$上连续
2. 在开区间$a,b$上可导
3. 对于任一$x \in a,b$使得$F'x \neq 0$

那么在$a,b$内至少有一点$\xi$, 使得$\frac{fb - fa}{Fa - Fb} = \fracf'\xiF'\xi$

洛必达法则

如果当$x \rightarrow a$或者$x \rightarrow \infty$是，两个函数$fx$和$Fx$都趋于零或者趋于无穷大，那么极限$\lim_{x \rightarrow a}\frac{fx}{Fx}$可能存在，可能不存在，通常把这种极限叫做未定式

定理 设

1. 当$x \rightarrow a$时，函数$fx$及$Fx$都趋于零
2. 在点$a$的某去心领域内，$f'x$及$F'x$都存在且$F'x \neq 0$
3. $\lim_{x \rightarrow a}\frac{f'x}{F'x}$存在或者为无穷大

则
$$\lim_{x \rightarrow a}\frac{fx}{Fx} = \lim_{x \rightarrow a}\frac{f'x}{F'x}$$

在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法叫做洛必达法则

定理 设

1. 当$x \rightarrow \infty$时，函数$fx$及$Fx$都趋于零
2. 在$x \geq N$时，$f'x$及$F'x$都存在且$F'x \neq 0$
3. $\lim_{x \rightarrow \infty}\frac{f'x}{F'x}$存在或者为无穷大

则
$$\lim_{x \rightarrow \infty}\frac{fx}{Fx} = \lim_{x \rightarrow \infty}\frac{f'x}{F'x}$$

泰勒公式

对于一些复杂的函数，为了便于研究，往往希望用一些简单的函数来近似表达，由于用多项式表示的函数，只要对自变量进行有限次的加减乘三种运算，便能求出他的函数值，因此我们经常用多项式来近似表达函数

泰勒中值定理1： 如果函数$fx$在$x_0$处具有n阶导数，那么存在$x_0$的一个领域，对于该领域内的任一x,有
$fx = fx_0 + f'x_0x - x_0 + \frac{f''x_0}{2!}x - x_0^2 + ... + \frac{f^{n}x_0}{n!}x - x_0^n + R_nx$其中$R_nx = ox - x_0^n$

泰勒中值定理2 如果函数$fx$在$x_0$的某个去心领域$Ux_0$内具有$n+1$阶导数，那么对于任一$x \in Ux_0$存在
$$fx = fx_0 + f'x_0x - x_0 + \frac{f''x_0}{2!}x - x_0^2 + ... + \frac{f^{n}x_0}{n!}x - x_0^n + R_nx$$
其中$R_nx = \frac{f^{n + 1}\xi}{n + 1!}x - x_0^{n+1}$