导数的应用

函数单调性的判定

设函数$y = fx$在$[a,b]$上连续，在$a,b$内可导

1. 如果在$a,b$内$f'x \geq 0$且等号仅在有限多个点处成立，那么函数$y = fx$在$[a,b]$上单调增加
2. 如果在$a,b$内$f'x \leq 0$且等号仅在有限多个点处成立，那么函数$y = fx$在$[a,b]$上单调减少

一般的，如果函数$fx$在定义区间上连续，除去有限个导数不存在的点外导数存在且在区间内只有有限个驻点，那么只要用函数的驻点以及导数不存在的点来划分函数的定义区间，就能保证$f'x$在各个部分区间内保持固定符号，因而函数$fx$在每个部分区间上单调

曲线的凹凸点以及拐点

从下图我们可以看到，在有的曲线弧上，如果任取两点，则联结这两点间的弦点位于弧段的上方或者下方

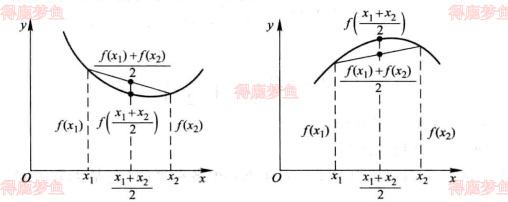
定义：设$fx$在区间I上是连续的，如果对I上任意两点$x_1, x_2$恒有$\frac{x_1 + x_2}{2} < \frac{fx_1 + fx_2}{2}$那么称$fx$在I上的图形是（向上）凹的，如果恒有$\frac{x_1 + x_2}{2} > \frac{fx_1 + fx_2}{2}$么称$fx$在I上的图形是（向下）凸的

定理：设$fx$在$[a,b]$上连续的，在a,b内具有一阶和二阶导数，那么

1. 若在a,b内有$f''x > 0$则$fx$在$[a,b]$上的图形是凹的
2. 若在a,b内有$f''x < 0$则$fx$在$[a,b]$上的图形是凸的

函数的极值

定义：设函数$fx$在点$x_0$的某领域$Ux_0$内有定义，如果去心领域内的任一x有$fx < fx_0$或者$fx > fx_0$那么就称$fx_0$为函数$fx$的一个极大值或者极小值

函数的极大值与极小值统称为函数的极值，使得函数取得极值的点称为极值点

定理1： 设函数$fx$在$x_0$处可导，且在$x_0$处取得极值，则$f'x = 0$
定理2： 设函数$fx$在$x_0$处连续，且在$x_0$的某去心领域内可导，

1. 若$x \in x_0 - \delta, x_0$时，$f'x > 0$而$x \in x_0, x_0 + \delta$时，$f'x < 0$则在$x_0$处取得极大值
2. 若$x \in x_0 - \delta, x_0$时，$f'x < 0$而$x \in x_0, x_0 + \delta$时，$f'x > 0$则在$x_0$处取得极小值
3. 若$x \in x_0 - \delta, x_0, x_0, x_0 + \delta$时，$f'x$的符号保持不变，则没有极值

定理3：设函数$fx$在$x_0$处具有二阶导数且$f'x_0 = 0$, $f''x_0 \neq 0$

1. 当$f''x_0 < 0$时，函数在$fx$在$x_0$取得极大值
2. 当$f''x_0 > 0$时，函数在$fx$在$x_0$取得极小值

函数图形的绘制

借助于一阶导数的符号，可以确定函数图形在哪个区间上上升，在哪个区间上下降；借助于二阶导数的符号，可以确定函数图形在哪个区间上为凹，在哪个区间上为凸，在什么地方有拐点.知道了函数图形的升降、凹凸以及拐点后，也就可以掌握函数的性态，并把函数的图形画得比较准确

一般步骤

1. 确定函数$y=fx$的定义域及函数所具有的某些特性（如奇偶性、周期性等），并求出函数的一阶导数$f'x$和二阶导数$f"x$
2. 求出一阶导数$f'x$和二阶导数$f"x$在函数定义域内的全部零点，并求出函数$fx$的间断点及$f'x$和$f"x$不存在的点，用这些点把函数的定义域划分成几个部分区间
3. 确定在这些部分区间内$f'x$和$f"x$的符号，并由此确定函数图形的升降、凹凸和拐点
4. 确定函数图形的水平、铅直渐近线以及其他变化趋势
5. 算出$f'x$和$f"x$的零点以及不存在的点所对应的函数值，定出图形上相应的点